Fit with a Thiele-Innes Basis
This example shows how to fit relative astrometry using a Thiele-Innes orbital basis instead of the traditional Campbell basis used in other tutorials. The Thiele-Innes basis is more suitable then Campbell for fitting low-eccentricity orbits, because it does not have the issues where ω, Ω, and tp become degenerate as eccentricity and/or inclination fall to zero.
At the end, we will convert our results back into the Campbell basis to compare.
using Octofitter
using CairoMakie
using PairPlots
using Distributions
astrom_like = PlanetRelAstromLikelihood(
(epoch = 50000, ra = -505.7637580573554, dec = -66.92982418533026, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50120, ra = -502.570356287689, dec = -37.47217527025044, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50240, ra = -498.2089148883798, dec = -7.927548139010479, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50360, ra = -492.67768482682357, dec = 21.63557115669823, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50480, ra = -485.9770335870402, dec = 51.147204404903704, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50600, ra = -478.1095526888573, dec = 80.53589069730698, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50720, ra = -469.0801731788123, dec = 109.72870493064629, σ_ra = 10, σ_dec = 10, cor=0),
(epoch = 50840, ra = -458.89628893460525, dec = 138.65128697876773, σ_ra = 10, σ_dec = 10, cor=0),
)
@planet b ThieleInnesOrbit begin
e ~ Uniform(0.0, 0.5)
A ~ Normal(0, 1000) # milliarcseconds
B ~ Normal(0, 1000) # milliarcseconds
F ~ Normal(0, 1000) # milliarcseconds
G ~ Normal(0, 1000) # milliarcseconds
θ ~ UniformCircular()
tp = θ_at_epoch_to_tperi(system,b,50000.0) # reference epoch for θ. Choose an MJD date near your data.
end astrom_like
@system TutoriaPrime begin
M ~ truncated(Normal(1.2, 0.1), lower=0.1)
plx ~ truncated(Normal(50.0, 0.02), lower=0.1)
end b
model = Octofitter.LogDensityModel(TutoriaPrime)LogDensityModel for System TutoriaPrime of dimension 9 and 9 epochs with fields .ℓπcallback and .∇ℓπcallback
Initialize the starting points, and confirm the data are entered correcly:
init_chain = initialize!(model)
octoplot(model, init_chain)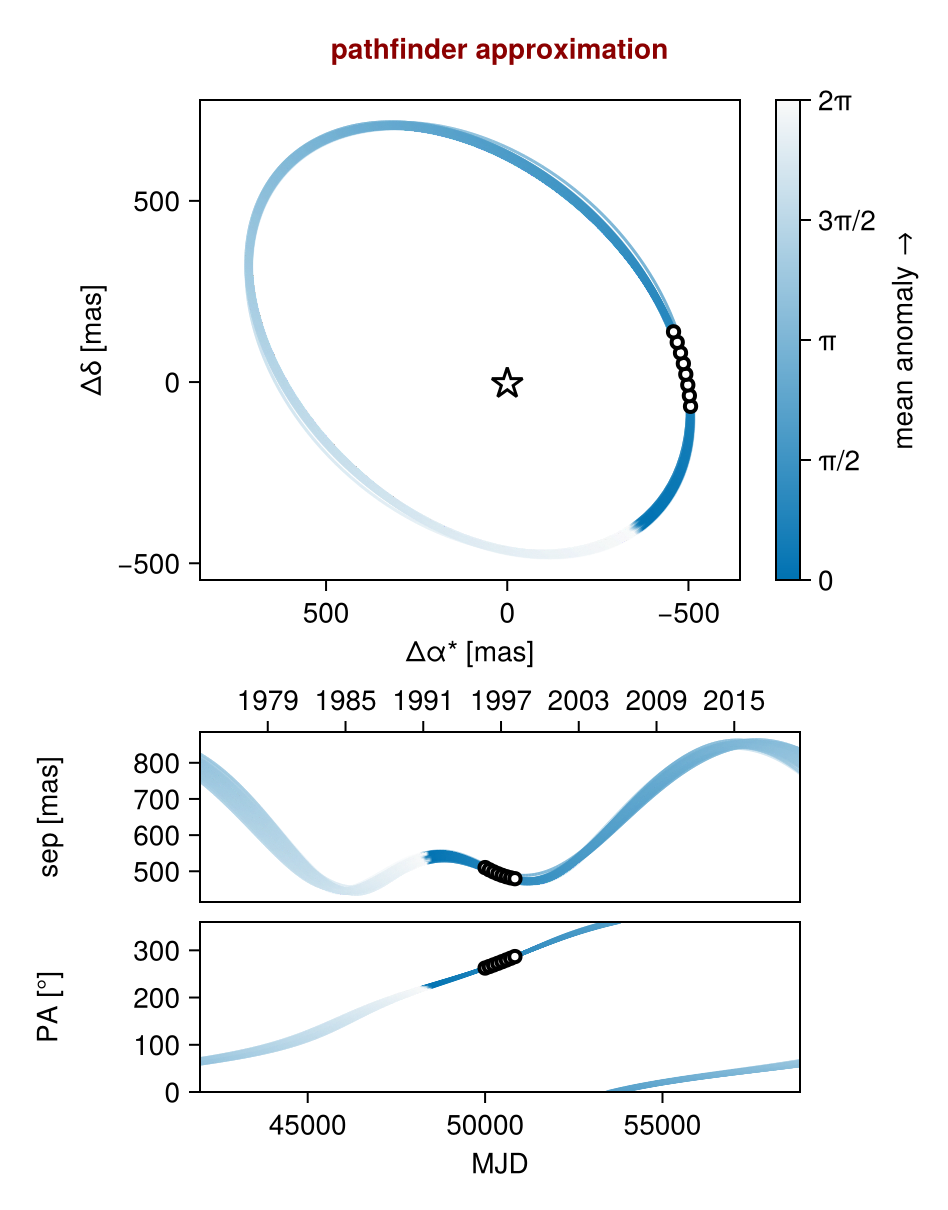
We now sample from the model as usual:
results = octofit(model)Chains MCMC chain (1000×24×1 Array{Float64, 3}):
Iterations = 1:1:1000
Number of chains = 1
Samples per chain = 1000
Wall duration = 4.59 seconds
Compute duration = 4.59 seconds
parameters = M, plx, b_e, b_A, b_B, b_F, b_G, b_θy, b_θx, b_θ, b_tp
internals = n_steps, is_accept, acceptance_rate, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size, is_adapt, loglike, logpost, tree_depth, numerical_error
Summary Statistics
parameters mean std mcse ess_bulk ess_tail ⋯
Symbol Float64 Float64 Float64 Float64 Float64 Fl ⋯
M 1.2107 0.0936 0.0036 681.6867 681.4476 1 ⋯
plx 50.0003 0.0207 0.0006 1034.3689 562.6804 1 ⋯
b_e 0.2860 0.1364 0.0083 305.4062 434.2079 0 ⋯
b_A 100.3081 637.2560 49.0848 189.0836 424.3160 1 ⋯
b_B -473.6527 350.8787 35.7375 119.6351 132.9017 1 ⋯
b_F 712.9445 587.9079 57.3751 110.2347 162.0680 1 ⋯
b_G 186.0687 370.4414 28.8614 172.4034 333.0541 1 ⋯
b_θy -0.1291 0.0180 0.0007 682.7860 502.0106 0 ⋯
b_θx -0.9951 0.0905 0.0038 588.1140 421.9572 0 ⋯
b_θ -1.6998 0.0133 0.0005 672.7733 573.1526 0 ⋯
b_tp 29373.9825 22348.6271 1452.9948 322.9448 522.9828 1 ⋯
2 columns omitted
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97.5% ⋯
Symbol Float64 Float64 Float64 Float64 Float64 ⋯
M 1.0349 1.1467 1.2135 1.2726 1.3888 ⋯
plx 49.9607 49.9866 49.9998 50.0129 50.0426 ⋯
b_e 0.0297 0.1767 0.3046 0.4040 0.4882 ⋯
b_A -923.1253 -455.0437 89.4682 672.0951 1175.5041 ⋯
b_B -978.5720 -724.5082 -542.8754 -288.2079 414.4094 ⋯
b_F -504.5368 340.6642 709.4898 1156.0349 1819.2821 ⋯
b_G -494.6794 -141.3835 255.8782 521.4100 701.1710 ⋯
b_θy -0.1657 -0.1407 -0.1277 -0.1165 -0.0969 ⋯
b_θx -1.1799 -1.0513 -0.9937 -0.9343 -0.8253 ⋯
b_θ -1.7261 -1.7082 -1.7000 -1.6906 -1.6737 ⋯
b_tp -23199.8510 14752.7395 36400.3264 48361.5739 49711.3170 ⋯
Notice that the fit was very very fast! The Thiele-Innes orbital paramterization is easier to explore than the default Campbell in many cases.
We now display the results:
octoplot(model,results)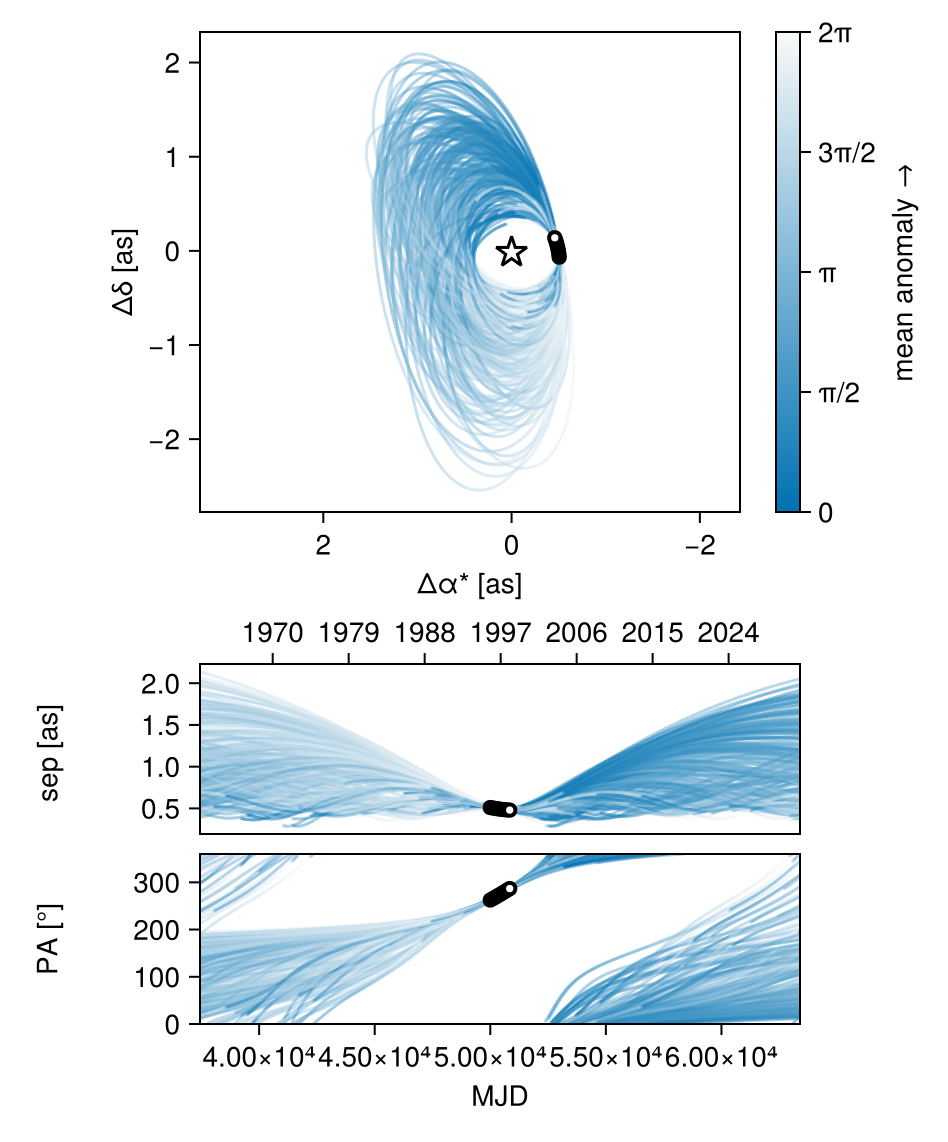
octocorner(model, results, small=false)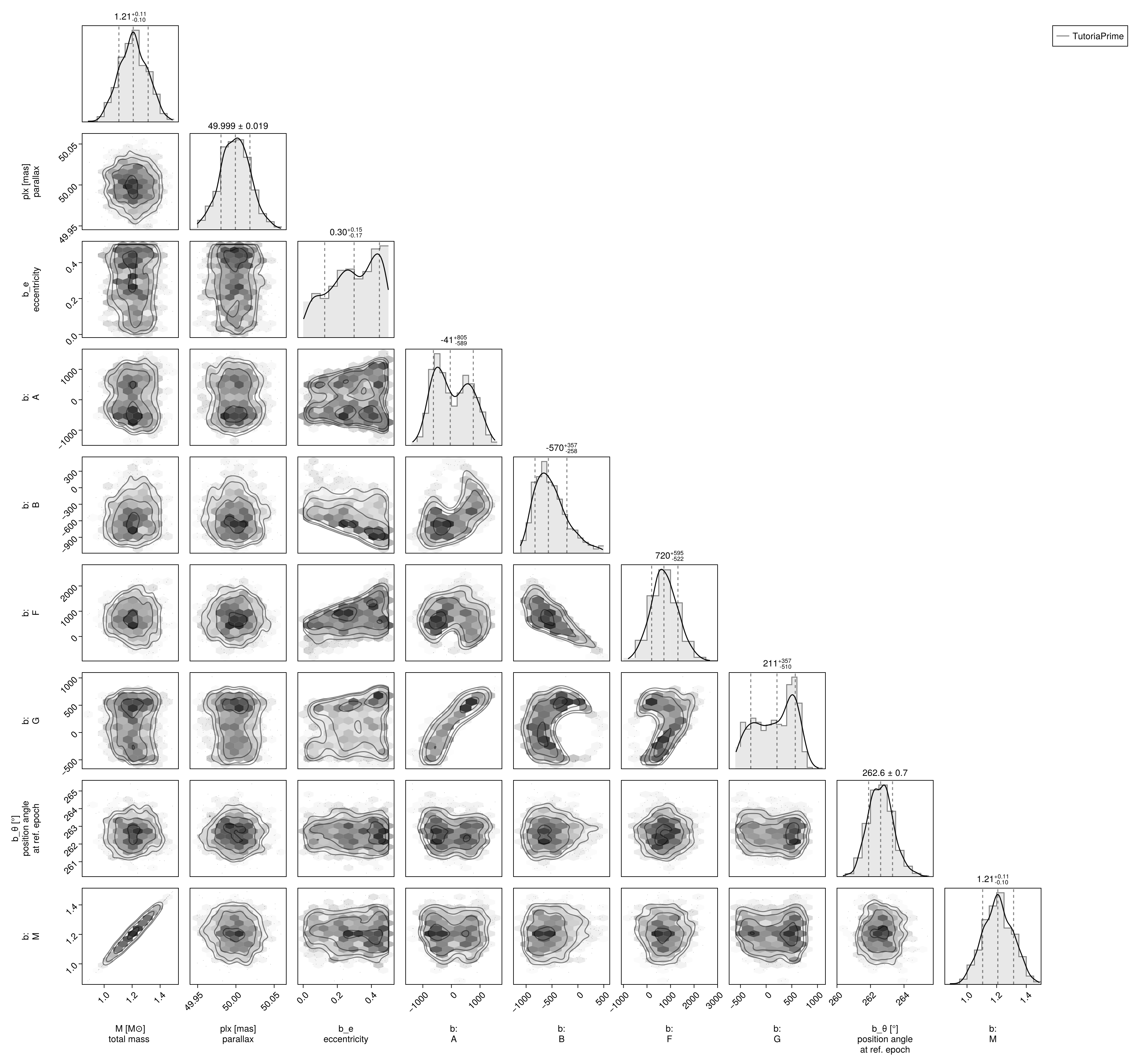
Conversion back to Campbell Elements
To convert our chain into the more familiar Campbell parameterization, we have to do a few steps. We start by turning the chain table into a an array of orbit objects, and then convert their type:
orbits_ti = Octofitter.construct_elements(model, results, :b, :) # colon means all rows1000-element Vector{ThieleInnesOrbit{Float64}}:
ThieleInnesOrbit{Float64}(0.30173200192322286, 11089.38799544613, 1.1645555892026769, 50.01196978471201, 1228.0710907833295, -210.8976248612639, 390.28667931501565, 549.3602852634285, 6.612251028412913, -21.97539428615863, 44297.51339279478, 0.051807274442195364, 1.365368004553625)
ThieleInnesOrbit{Float64}(0.4031161151910368, -21936.788369273185, 1.1497879115132887, 50.028663879392695, 1288.886320800711, -310.865840732006, 1268.7765261496127, 775.8631024618461, -25.59326881695121, 21.763883647919904, 76174.55225709663, 0.03012729796824689, 1.5332108344238244)
ThieleInnesOrbit{Float64}(0.432683662086737, -27836.975465622236, 1.1543429654916013, 50.001639599078125, 1292.9899328519589, -366.8517868699749, 1393.0114915568192, 784.0338613014454, -27.80942807721035, 21.76853619020969, 81771.7265922678, 0.028065121394469233, 1.5891412785500627)
ThieleInnesOrbit{Float64}(0.47058693680033725, -32420.855925339536, 1.146914908041544, 50.00058672881315, 1305.4534384313718, -446.0756884708129, 1470.517996410356, 808.425405430298, -28.85025976518198, 21.615573358101376, 86023.40004041386, 0.02667801356804291, 1.6666638869326291)
ThieleInnesOrbit{Float64}(0.13622825018729132, 24741.363367242964, 1.3565513599196766, 49.99202089755308, 138.81315571794076, -528.7289736905637, 885.0539727400256, 340.418657079319, -15.568733617354921, -1.4683355119980956, 26023.72347409261, 0.08818620577996913, 1.1469204421476813)
ThieleInnesOrbit{Float64}(0.06574538901731933, 49221.48984676004, 1.2659276237853696, 50.01130688175469, -294.9616722597943, -515.2598514681098, 641.7131931871052, -131.7916883659473, -8.137415361870424, -5.963512965196959, 17725.992285092078, 0.12946713484567124, 1.068056201882025)
ThieleInnesOrbit{Float64}(0.43382003007127407, 48562.50789777614, 1.236653872503406, 50.009083770980105, -727.4411976897361, -933.3875931395256, 1267.158584295372, -60.349969065181725, -19.75709421959844, -17.51551232531825, 56216.95700123098, 0.04082279717482915, 1.591365985449369)
ThieleInnesOrbit{Float64}(0.3692023735214343, -5683.793145190408, 1.2570007966930914, 50.00526700846192, 12.819929419826263, -789.4907704104304, 1488.533088986413, 364.3227468659668, -26.574197833352656, -4.041363582887879, 55989.979161121475, 0.040988288758658946, 1.4732918838604154)
ThieleInnesOrbit{Float64}(0.3862707255460924, -1229.9841757735703, 1.2679122774514728, 50.0085438073341, 476.370271367606, -632.9622487880799, 1363.7584979059084, 544.4556306816153, -25.193453762151258, 4.841415215865263, 52662.47403884643, 0.04357815456513662, 1.5029191092009275)
ThieleInnesOrbit{Float64}(0.4344969965413904, -880.2203212308232, 1.1966091002765455, 50.0163220990469, 900.0732496738771, -488.3080562515471, 1122.5464699688775, 719.4434801236529, -21.13776732973069, 12.4636421583911, 53302.362403207306, 0.04305500413072223, 1.5926940723305218)
⋮
ThieleInnesOrbit{Float64}(0.2563790181442335, 47809.58865975535, 1.2227337715873776, 50.027363142513664, -692.7342057844694, -490.2717593984237, 375.97477635212175, -408.47866139684146, -1.8549078883562782, -12.964356114143635, 23286.45285751037, 0.09855229765950291, 1.2998239051988416)
ThieleInnesOrbit{Float64}(0.10175779966189354, 48087.41457837827, 1.1952215409297906, 50.00632627285656, -475.84408561730027, -390.46554463573534, 239.76060773393507, -399.2335206593711, 2.0144639008408114, -8.297531035799027, 14717.409379892786, 0.15593324709596834, 1.1075066419083297)
ThieleInnesOrbit{Float64}(0.4135756353206301, 47894.96678194347, 1.1226272247207165, 50.00312840291843, -816.842569499015, -720.3198686293109, 528.9709800249389, -401.972754352008, -3.246305783219601, -17.56078786956417, 35623.01050511684, 0.06442278181732289, 1.5525783380207132)
ThieleInnesOrbit{Float64}(0.2395997055678268, 48763.7041776899, 1.1763527684130841, 50.01169111218759, -443.24172669050995, -563.1911914542884, 402.6385973185827, -315.585752234424, -0.029124976429296155, -10.03632771773428, 18269.3285498344, 0.1256167366626151, 1.276790357096132)
ThieleInnesOrbit{Float64}(0.34926976220220685, 1638.364150452413, 1.2483409649135977, 49.99956767199837, 847.7362641719818, -422.8988507454581, 1138.4858758967157, 637.4618611941098, -21.96491939230701, 12.666851005125713, 51075.01021502255, 0.044932608408413816, 1.4399549329929417)
ThieleInnesOrbit{Float64}(0.33960827444377917, -3431.822653306728, 1.265136055108723, 49.977224312605706, 787.9150203297584, -480.8327266390711, 1296.9588240828975, 610.5697703647609, -24.87892063466236, 11.720369815318604, 56009.13145710652, 0.04097427283272323, 1.4242561359820591)
ThieleInnesOrbit{Float64}(0.1236530096934949, 33403.18206079007, 1.1608291290648405, 50.03939881611976, 600.9381534630799, -288.25742275567137, 426.5820823626177, 458.08935416584694, -6.345830209295452, 7.822845914039328, 19212.07990967198, 0.11945262794227712, 1.1323431571448201)
ThieleInnesOrbit{Float64}(0.24837250092931074, 27697.936771764165, 1.0713296074574084, 50.04243744652455, 536.0374714504354, -413.4109469587512, 626.8047705425837, 487.19155481770184, -9.905384689304887, 5.425427354882977, 24226.290363161825, 0.09472904844470077, 1.288756196170073)
ThieleInnesOrbit{Float64}(0.2961925454941147, 36544.47174919262, 1.2206013065996402, 49.990939662325076, 666.6343651482977, 164.23492041265328, -196.34680506318804, 473.87354827246355, 2.2579429830739457, 9.403989442547859, 17166.683177908235, 0.1336853141438929, 1.3570874320185147)Here is one of those entries:
display(orbits_ti[1])We can now make a table of results (and visualize them in a corner plot) by querying properties of these objects:
table = (;
B_a = semimajoraxis.(orbits_ti),
B_e = eccentricity.(orbits_ti),
B_i = rad2deg.(inclination.(orbits_ti)),
)
pairplot(table)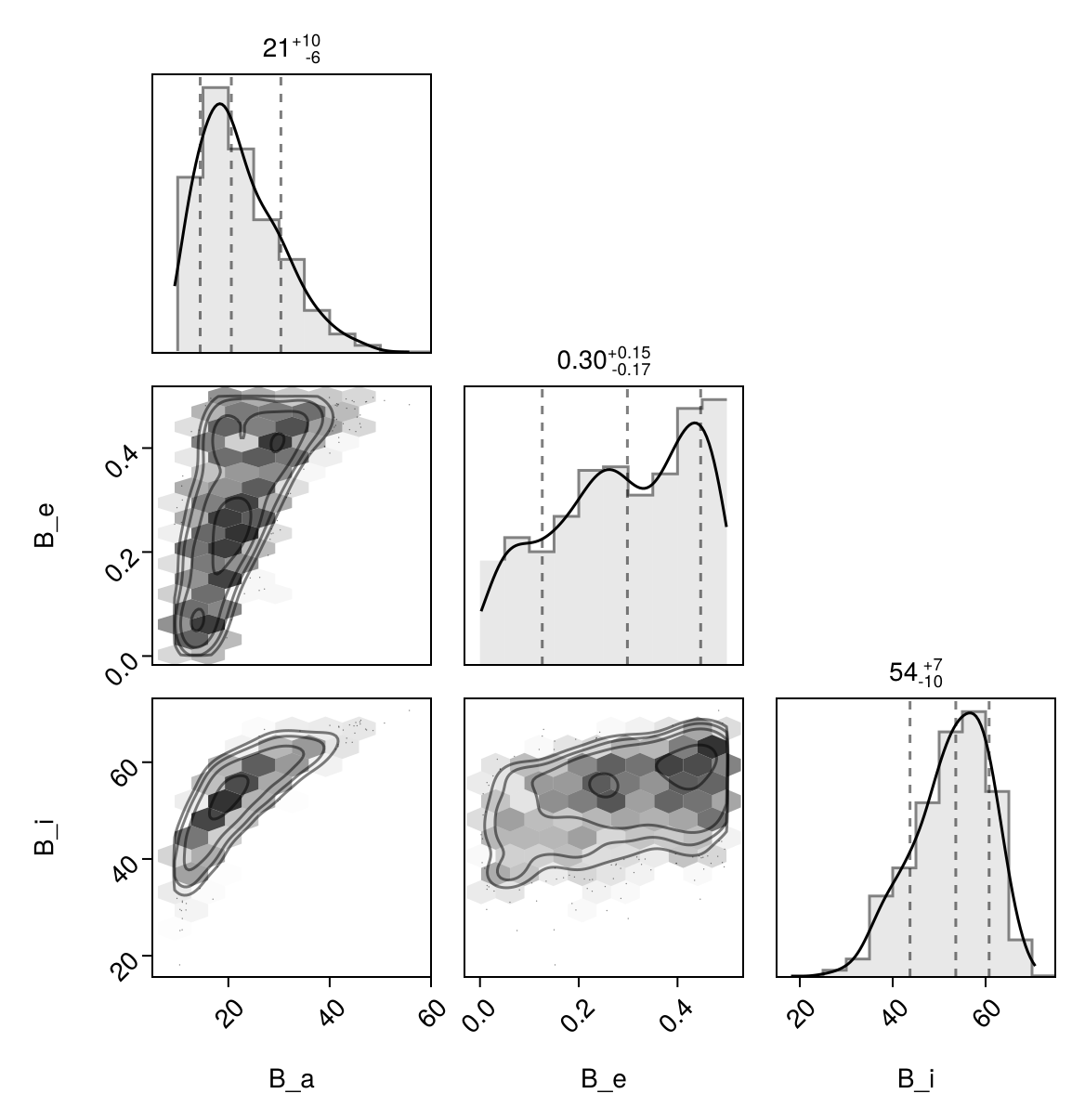
We can also convert the orbit objects into Campbell parameters:
orbits_campbell = Visual{KepOrbit}.(orbits_ti)
orbits_campbell[1]KepOrbit{Float64}
─────────────────────────
a [au ] = 25.8
e = 0.301732
i [° ] = 62.9
ω [° ] = 523.0
Ω [° ] = 178.0
tp [day] = 11100.0
M [M⊙ ] = 1.16
period [yrs ] : 121.3
mean motion [°/yr] : 2.97
──────────────────────────
plx [mas] = 50.0
distance [pc ] : 20.0
──────────────────────────