Posterior Predictive Checks
A posterior predictive check compares our true data with simulated data drawn from the posterior. This allows us to evaluate if the model is able to reproduce our observations appropriately. Samples drawn from the posterior predictive distribution should match the locations of the original data.
To demonstrate, we will fit a model to relative astrometry data:
using Octofitter
using Distributions
astrom_dat = Table(
epoch= [50000,50120,50240,50360,50480,50600,50720,50840,],
ra = [-505.764,-502.57,-498.209,-492.678,-485.977,-478.11,-469.08,-458.896,],
dec = [-66.9298,-37.4722,-7.92755,21.6356, 51.1472, 80.5359, 109.729, 138.651,],
σ_ra = fill(10.0, 8),
σ_dec = fill(10.0, 8),
cor = fill(0.0, 8)
)
astrom_like = PlanetRelAstromLikelihood(astrom_dat, name="simulated astrom")
planet_b = Planet(
name="b",
basis=Visual{KepOrbit},
likelihoods=[astrom_like],
variables=@variables begin
a ~ truncated(Normal(10, 4), lower=0.1, upper=100)
e ~ Uniform(0.0, 0.5)
i ~ Sine()
ω ~ UniformCircular()
Ω ~ UniformCircular()
θ ~ UniformCircular()
tp = θ_at_epoch_to_tperi(θ,50420; system.M, a, e, i, ω, Ω) # reference epoch for θ. Choose an MJD date near your data.
end
)
sys = System(
name="Tutoria",
companions=[planet_b],
likelihoods=[],
variables=@variables begin
M ~ truncated(Normal(1.2, 0.1), lower=0.1)
plx ~ truncated(Normal(50.0, 0.02), lower=0.1)
end
)
model = Octofitter.LogDensityModel(sys)
using Random
Random.seed!(0)
chain = octofit(model)Chains MCMC chain (1000×28×1 Array{Float64, 3}):
Iterations = 1:1:1000
Number of chains = 1
Samples per chain = 1000
Wall duration = 3.5 seconds
Compute duration = 3.5 seconds
parameters = M, plx, b_a, b_e, b_i, b_ωx, b_ωy, b_Ωx, b_Ωy, b_θx, b_θy, b_ω, b_Ω, b_θ, b_tp
internals = n_steps, is_accept, acceptance_rate, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size, is_adapt, loglike, logpost, tree_depth, numerical_error
Summary Statistics
parameters mean std mcse ess_bulk ess_tail r ⋯
Symbol Float64 Float64 Float64 Float64 Float64 Floa ⋯
M 1.1821 0.0949 0.0034 768.1107 576.2198 1.0 ⋯
plx 49.9996 0.0196 0.0005 1474.4368 654.8202 1.0 ⋯
b_a 11.6641 2.1484 0.1417 212.5453 425.2264 1.0 ⋯
b_e 0.1405 0.1012 0.0053 368.9211 392.1304 1.0 ⋯
b_i 0.6335 0.1531 0.0099 258.1252 248.3632 1.0 ⋯
b_ωx 0.0038 0.7149 0.0534 208.0390 699.7637 1.0 ⋯
b_ωy -0.0769 0.7054 0.0517 201.9895 543.4901 1.0 ⋯
b_Ωx -0.2095 0.7151 0.0928 74.9446 298.4757 1.0 ⋯
b_Ωy -0.1845 0.6564 0.0896 68.2649 359.0669 1.0 ⋯
b_θx 0.0747 0.0105 0.0004 878.6689 630.9839 0.9 ⋯
b_θy -1.0021 0.1009 0.0035 858.9123 551.0444 1.0 ⋯
b_ω -0.2666 1.7822 0.1134 300.5113 645.1110 1.0 ⋯
b_Ω -0.9827 1.7900 0.2160 112.1317 218.4142 1.0 ⋯
b_θ -1.4964 0.0073 0.0002 934.5854 641.3347 1.0 ⋯
b_tp 42792.9699 5011.3533 316.6178 237.4203 470.0924 1.0 ⋯
2 columns omitted
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97.5%
Symbol Float64 Float64 Float64 Float64 Float64
M 1.0016 1.1199 1.1828 1.2411 1.3750
plx 49.9603 49.9862 49.9992 50.0137 50.0382
b_a 8.3480 10.0972 11.2598 12.9488 16.5075
b_e 0.0070 0.0635 0.1191 0.2032 0.3757
b_i 0.2907 0.5416 0.6458 0.7415 0.8884
b_ωx -1.0691 -0.6843 0.0009 0.7202 1.0481
b_ωy -1.0505 -0.7658 -0.1363 0.5886 1.0740
b_Ωx -1.0854 -0.8424 -0.4205 0.4589 1.0509
b_Ωy -1.0670 -0.7483 -0.3475 0.3709 1.0263
b_θx 0.0554 0.0675 0.0742 0.0813 0.0971
b_θy -1.2141 -1.0644 -0.9986 -0.9341 -0.8162
b_ω -2.9751 -1.9530 -0.3123 1.1381 2.9544
b_Ω -3.0144 -2.5143 -1.8051 0.5127 2.9413
b_θ -1.5104 -1.5012 -1.4964 -1.4916 -1.4824
b_tp 30799.4910 40091.7572 43748.8994 46457.6653 49776.6869
We now have our posterior as approximated by the MCMC chain. Convert these posterior samples into orbit objects:
# Instead of creating orbit objects for all rows in the chain, just pick
# every twentieth row.
ii = 1:20:1000
orbits = Octofitter.construct_elements(model, chain, :b, ii)50-element Vector{Visual{KepOrbit{Float64}, Float64}}:
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.96, 0.146, 0.538, -2.14, 3.64, 44700.0, 1.2), 49.98615809188959, 4.1264384805873577e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.5, 0.0798, 0.538, -2.24, 4.39, 46500.0, 1.27), 49.973050541965925, 4.127520813921118e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(8.59, 0.197, 0.589, 3.06, 4.54, 45600.0, 1.23), 50.02191526973248, 4.1234887775659426e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(13.8, 0.0122, 0.783, 2.74, 3.34, 37300.0, 1.3), 49.99349107718122, 4.1258332195417103e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(11.6, 0.0091, 0.704, -1.67, 3.98, 44700.0, 1.06), 49.98180890535762, 4.1267975442358702e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.82, 0.186, 0.585, -2.11, 3.51, 44000.0, 1.0), 50.06796943692027, 4.1196958567885533e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(15.5, 0.0642, 0.861, -0.925, 0.264, 33200.0, 1.32), 50.0234326064724, 4.123363701762608e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(14.5, 0.338, 0.638, 0.416, 4.86, 32500.0, 1.16), 50.00721509350455, 4.1247009228851893e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.6, 0.179, 0.437, 1.75, 5.13, 43500.0, 1.24), 49.99183676973666, 4.1259697497644653e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(13.6, 0.0591, 0.726, 1.9, 3.51, 34700.0, 1.17), 49.99760817979972, 4.1254934737144583e6)
⋮
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.93, 0.0853, 0.625, -2.01, 4.14, 45800.0, 1.13), 49.984473884654996, 4.1265775193128265e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(12.9, 0.0381, 0.704, -1.2, 0.408, 36300.0, 1.18), 49.985418109039045, 4.126499568277028e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(12.3, 0.089, 0.721, -0.0826, 3.93, 48200.0, 1.08), 49.98405411946963, 4.126612174236438e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(10.5, 0.0107, 0.542, -1.94, 4.09, 45600.0, 1.23), 49.99493424182435, 4.1257141223428403e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(11.2, 0.0253, 0.608, -0.599, 3.87, 47200.0, 1.11), 50.0084925686493, 4.1245955567236054e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(10.2, 0.228, 0.382, -2.46, 2.99, 42300.0, 1.19), 49.98452898043077, 4.126572970765619e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(12.1, 0.224, 0.532, -2.76, 2.18, 36700.0, 1.03), 50.00751323261129, 4.124676331887373e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(11.0, 0.149, 0.424, 0.0875, 6.27, 40100.0, 1.04), 50.022812922367024, 4.1234147821156983e6)
Visual{KepOrbit{Float64}, Float64}(KepOrbit(9.23, 0.179, 0.478, 0.56, 0.771, 44900.0, 1.18), 50.00512288451952, 4.1248734999299715e6)Calculate and plot the location the planet would be at each observation epoch:
using CairoMakie
epochs = astrom_like.table.epoch' # transpose
x = raoff.(orbits, epochs)[:]
y = decoff.(orbits, epochs)[:]
fig = Figure()
ax = Axis(
fig[1,1], xlabel="ra offset [mas]", ylabel="dec offset [mas]",
xreversed=true,
aspect=1
)
for orbit in orbits
Makie.lines!(ax, orbit, color=:lightgrey)
end
Makie.scatter!(
ax,
x, y,
markersize=3,
)
fig
Makie.scatter!(ax, astrom_like.table.ra, astrom_like.table.dec,color=:black, label="observed")
Makie.scatter!(ax, [0],[0], marker='⋆', color=:black, markersize=20,label="")
Makie.xlims!(400,-700)
Makie.ylims!(-200,200)
fig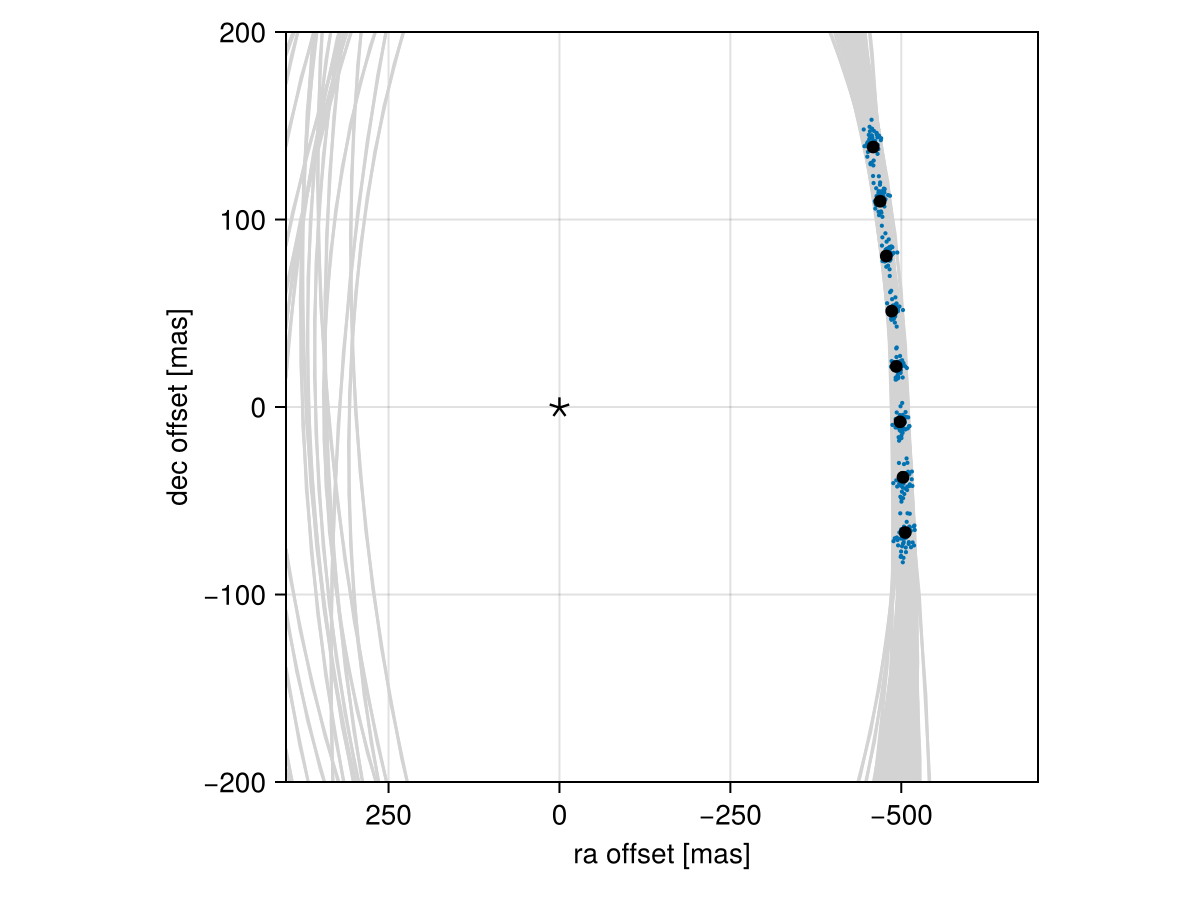
Looks like a great match to the data! Notice how the uncertainty around the middle point is lower than the ends. That's because the orbit's posterior location at that epoch is also constrained by the surrounding data points. We can know the location of the planet in hindsight better than we could measure it!
You can follow this same procedure for any kind of data modelled with Octofitter.