Fitting Likelihood Maps

There are circumstances where you might have a 2D map of planet likelihood vs. position in the plane of the sky ($\Delta$ R.A. and Dec.). These could originate from:

• cleaned interferometer data
• some kind of spectroscopic cube model fitting to detect planets
• some other imaginative modelling process I haven't thought of!

You can feed such 2D likelihood maps in to Octofitter. Simply pass in a list of maps and a platescale mapping the pixel size to a separation in milliarcseconds. You can of course also mix these likelihood maps with relative astrometry, radial velocity, proper motion, images, etc.

If your likelihood map is not centered on the star, you can specify offset dimensions as shown below.

using Octofitter
using Distributions
using OctofitterImages
using Pigeons
using AstroImages

Typically one would load your likelihood maps from eg. FITS files like so:

# If centred at the star:
image1 = AstroImages.recenter(AstroImages.load("image-example-1.fits",1))

# If not centered at the star:
image1 = AstroImages.load("image-example-1.fits")
image1_offset = AstroImage(
    image1,
    # Specify coordinates here:
    (
        # X coordinates should go from negative to positive.
        # The image should have +RA at the left.
        X(-4.85878653527304:1.0:95.14121346472696),
        Y(-69.0877222942365:1.0:30.9122777057635)
    )
    # Below, there is a platescale option. `platescale` multiplies
    # these values by a scaling factor. It can be 1 if the coordinates
    # above are already in milliarcseconds.
)
imview(image1_offset)

If you're using a FITS file, make sure to store your data in 64-bit floating point format.

For this demonstration, however, we will construct two synthetic likelihood maps using a template orbit. We will create three peaks in two epochs.

orbit_template = orbit(
    a = 1.0,
    e = 0.1,
    i = 0.0,
    ω = 0.0,
    Ω = 0.5,
    plx = 50.0,
    M = 1
)
epochs = [
    mjd("2024-01-30"),
    mjd("2024-02-29"),
]

## Create simulated data with three likelihood peaks at both epochs
x1,y1 = raoff(orbit_template,epochs[1]), decoff(orbit_template,epochs[1])
# The three peaks in our likelihood map
d1 = MvNormal([x1, y1], [
    5.0 0.2
    0.2 8.0
])
d2 = MvNormal([x1+8.0,y1+4], [
    5.0 0.6
    0.6 5.0
])
d3 = MvNormal([x1+9.0, y1-10.0], [
    6.0 0.6
    0.6 6.0
])
d = MixtureModel([d1, d2, d3], [0.5, 0.3, 0.2])

# Calculate a log-likelihood map over a +-50 mas patch around (x1, x2)
lm1 = broadcast(x1 .+ (-50:50), y1 .+ (-50:1:50)') do x, y
    logpdf(d, [x, y])
end

# Place in an AstroImage with appropriate offset coordinates
image1_offset = AstroImage(
    lm1,
    # Specify coordinates here:
    (
        # X coordinates should go from negative to positive.
        # The image should have +RA at the left.
        X(x1 .+ (-50:50)),
        Y(y1 .+ (-50:1:50))
    )
    # Below, there is a platescale option. `platescale` multiplies
    # these values by a scaling factor. It can be 1 if the coordinates
    # above are already in milliarcseconds.
)
imview(10 .^ image1_offset)

That was the first epoch. We now generate data for the second epoch:

x2,y2 = raoff(orbit_template,epochs[2]), decoff(orbit_template,epochs[2])
# The three peaks in our likelihood map
d1 = MvNormal([x2, y2], [
    5.0 0.2
    0.2 8.0
])
d2 = MvNormal([x2+10.0,y2], [
    5.0 0.6
    0.6 5.0
])
d3 = MvNormal([x2-4.0, y2-10.0], [
    6.0 0.6
    0.6 6.0
])
d = MixtureModel([d1, d2, d3], [0.5, 0.3, 0.2])



lm2 = broadcast(x2 .+ (-50:50), y2 .+ (-50:1:50)') do x, y
    logpdf(d, [x, y])
end
# Place in an AstroImage with appropriate offset coordinates
image2_offset = AstroImage(
    lm2,
    # Specify coordinates here:
    (
        # X coordinates should go from negative to positive.
        # The image should have +RA at the left.
        X(x2 .+ (-50:50)),
        Y(y2 .+ (-50:1:50))
    )
    # Below, there is a platescale option. `platescale` multiplies
    # these values by a scaling factor. It can be 1 if the coordinates
    # above are already in milliarcseconds.
)
imview(10 .^ image2_offset)

Okay, we have our synthetic data. We now set up a LogLikelihoodMap object to contain our matrices of log likelihood values:

loglikemap = LogLikelihoodMap(
    (;
        epoch=epochs[1],
        map=image1_offset,
        platescale=1.0 # milliarcseconds/pixel of the map
    ),
    (;
        epoch=epochs[2],
        map=image2_offset,
        platescale=1.0 # milliarcseconds/pixel of the map
    )
);

OctofitterImages.LogLikelihoodMap Table with 5 columns and 2 rows:
     epoch    map                   platescale  fillvalue  mapinterp
   ┌───────────────────────────────────────────────────────────────────────────
 1 │ 60339.0  [-393.192 -387.534 …  1.0         -423.544   101×101 extrapolate…
 2 │ 60369.0  [-287.052 -281.177 …  1.0         -423.544   101×101 extrapolate…

We now create a one-planet model and run the fit using octofit_pigeons. This parallel-tempered sampler is slower than the regular octofit, but is recommended over the default Hamiltonian Monte Carlo sampler due to the multi-modal nature of the data.

@planet b Visual{KepOrbit} begin
    a ~ Uniform(0, 10)
    e ~ Uniform(0.0, 0.5)
    i ~ Sine()
    ω ~ UniformCircular()
    Ω ~ UniformCircular()
    θ ~ UniformCircular()
    tp = θ_at_epoch_to_tperi(system,b,60339.0)  # reference epoch for θ. Choose an MJD date near your data.
end loglikemap
@system Tutoria begin
    M ~ truncated(Normal(1.0, 0.1), lower=0.1)
    plx ~ truncated(Normal(50.0, 0.02), lower=0.1)
end b
model = Octofitter.LogDensityModel(Tutoria)
chain, pt = octofit_pigeons(model, n_rounds=10) # increase n_rounds until log(Z₁/Z₀) converges.
display(chain)

┌ Warning: This model has priors that cannot be sampled IID.
└ @ OctofitterPigeonsExt ~/work/Octofitter.jl/Octofitter.jl/ext/OctofitterPigeonsExt/OctofitterPigeonsExt.jl:104
[ Info: Sampler running with multiple threads     : true
[ Info: Likelihood evaluated with multiple threads: false
[ Info: Determining initial positions using pathfinder, around that location.
┌ Warning: ErrorException("Could not find starting point within 0.001 - 0.999 quantiles of priors.")
└ @ Octofitter ~/work/Octofitter.jl/Octofitter.jl/src/initialization.jl:302
┌ Info: Found a sample of initial positions
└   initial_logpost_range = (-8.058787193370243, -8.058787193370243)
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
  scans     restarts      Λ        Λ_var      time(s)    allc(B)  log(Z₁/Z₀)   min(α)     mean(α)    min(αₑ)   mean(αₑ)
────────── ────────── ────────── ────────── ────────── ────────── ────────── ────────── ────────── ────────── ──────────
        2          0       2.27       2.09      0.204   3.73e+06      -34.2    5.7e-25      0.859          1          1
        4          0       1.92       2.69     0.0656   1.45e+05      -16.5   0.000619      0.851          1          1
        8          0       3.72       3.03      0.129   2.72e+05      -16.8      0.138      0.782          1          1
       16          0       3.68       3.58      0.258   5.13e+05      -18.8      0.374      0.766          1          1
       32          1       3.84       3.75      0.519   8.08e+05      -19.9      0.502      0.755          1          1
       64          6        3.6       3.03        1.1   4.57e+07      -21.2      0.536      0.786          1          1
      128         17       3.86          3       1.93   7.93e+07        -21      0.645      0.779          1          1
      256         33       3.61       3.11       3.98   1.59e+08        -21      0.661      0.783          1          1
      512         82       3.75       3.08       7.76   3.14e+08      -20.9      0.705       0.78          1          1
 1.02e+03        177       3.89       3.14       15.6   6.29e+08      -21.1      0.708      0.773          1          1
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────

Display the results:

octoplot(model, chain)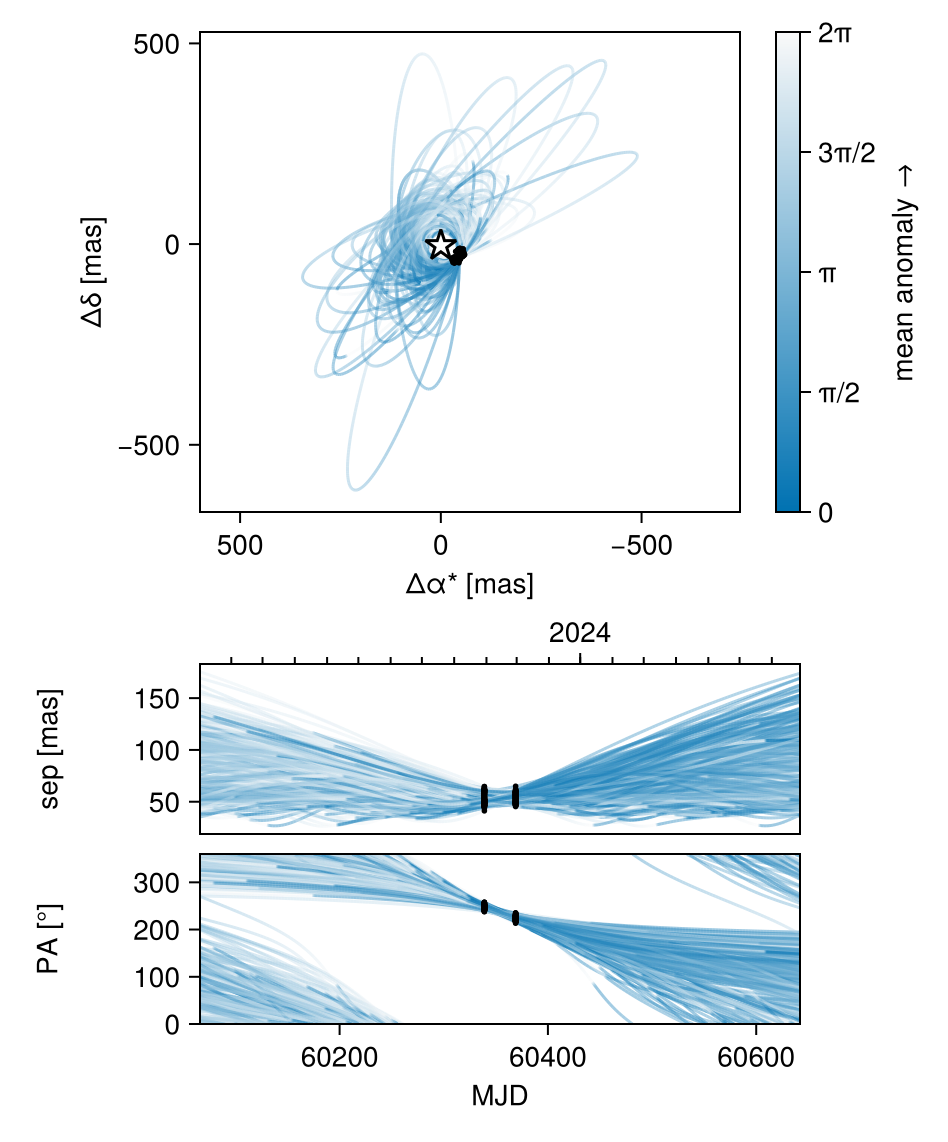

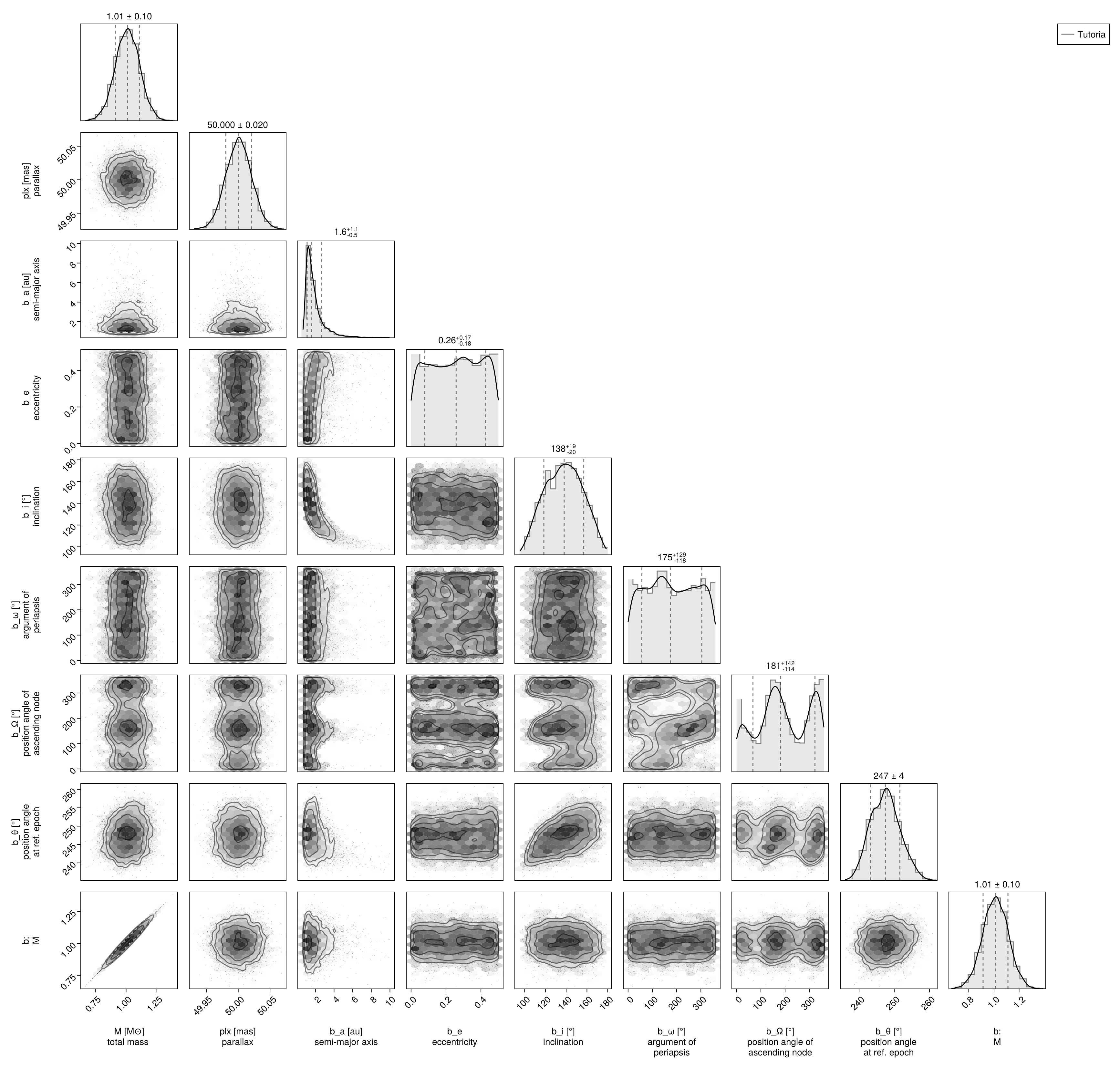
Corner plot:

using CairoMakie, PairPlots
octocorner(model,chain,small=true,)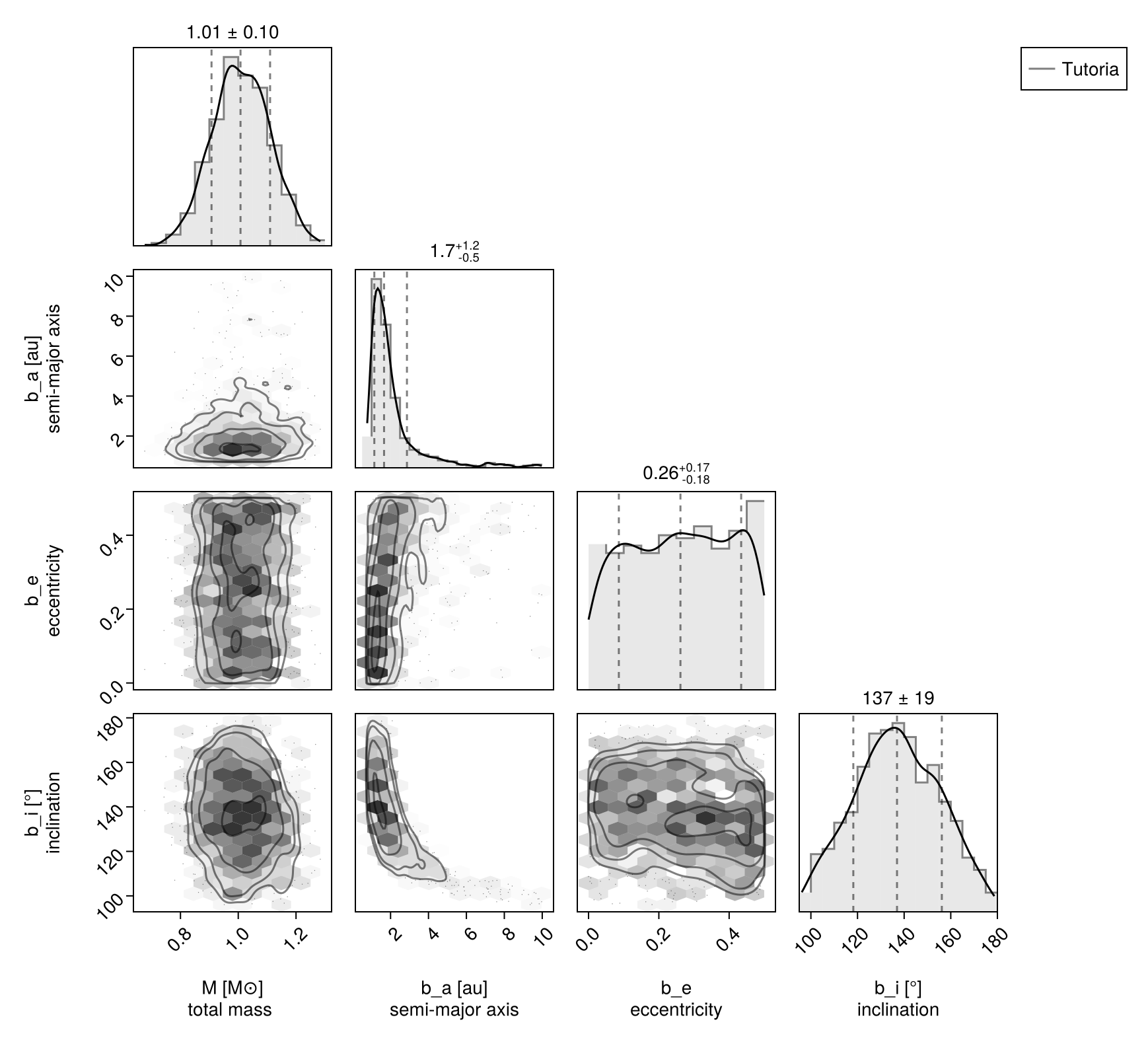

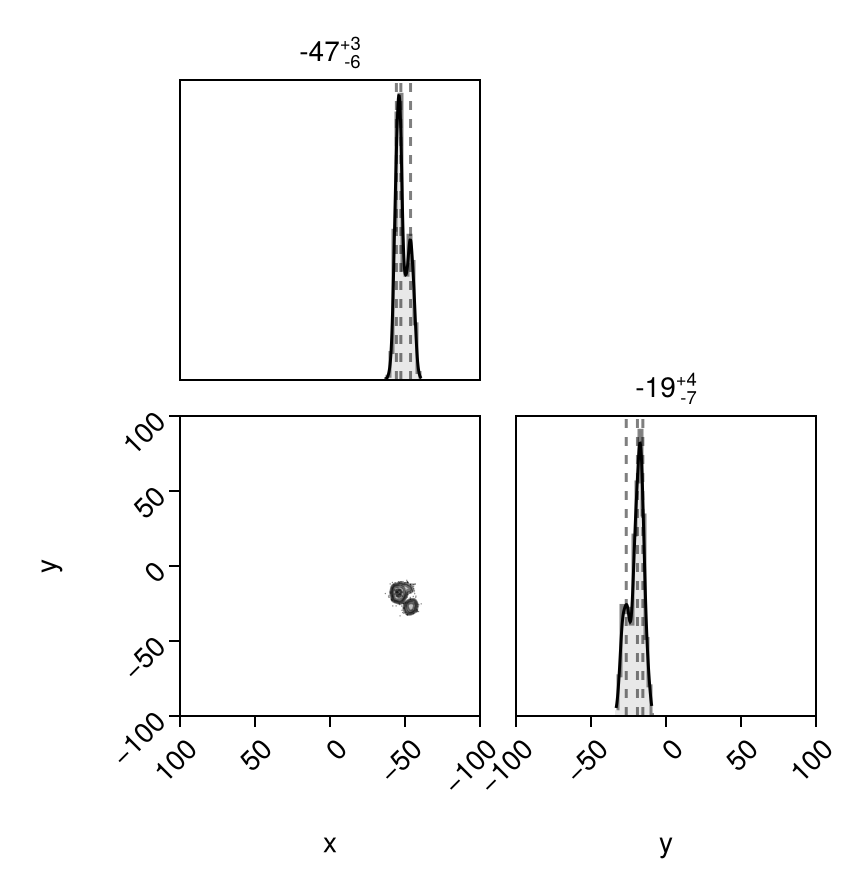
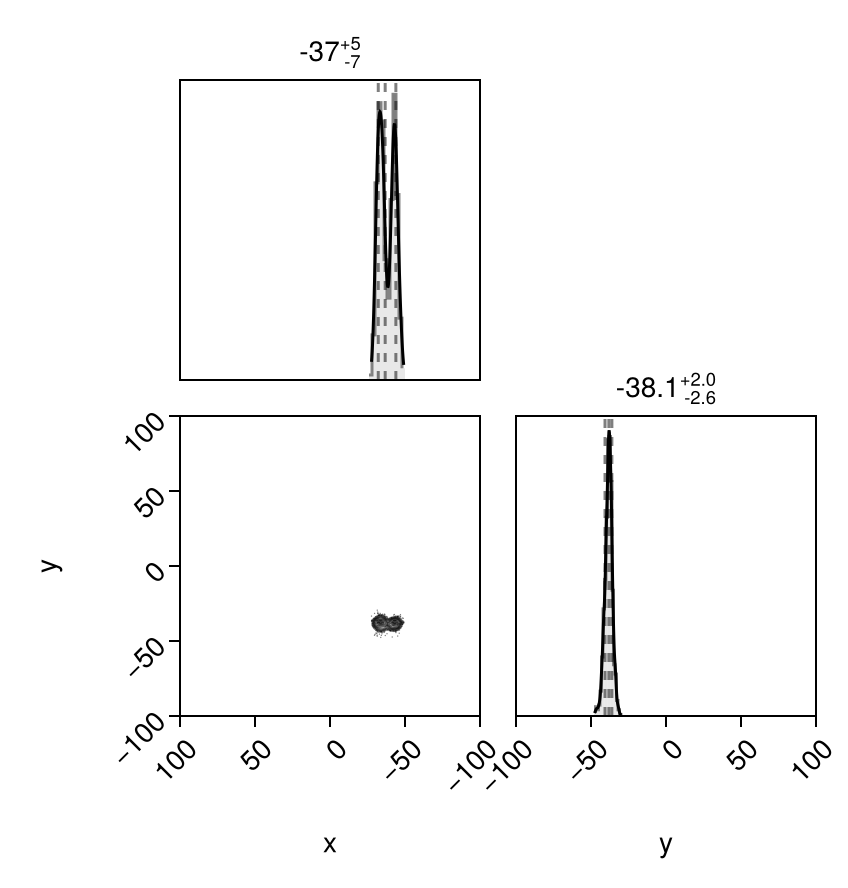
And finally let's look at the posterior predictive distributions at both epochs:

els = Octofitter.construct_elements(chain,:b, :)
x = raoff.(els, loglikemap.table.epoch[1])
y = decoff.(els, loglikemap.table.epoch[1])
pairplot(
    (;x,y),
    axis=(
        x = (;
            lims=(low=100,high=-100)
        ),
        y = (;
            lims=(low=-100,high=100)
        )
    )
)

x = raoff.(els, loglikemap.table.epoch[2])
y = decoff.(els, loglikemap.table.epoch[2])
pairplot(
    (;x,y),
    axis=(
        x = (;
            lims=(low=100,high=-100)
        ),
        y = (;
            lims=(low=-100,high=100)
        )
    )
)

Resume sampling for additional rounds

If you would like to add additional rounds of sampling, you may do the following:

pt = increment_n_rounds!(pt, 2)
chain, pt = octofit_pigeons(pt)

(chain = MCMC chain (4096×19×1 Array{Float64, 3}), pt = PT(checkpoint = false, ...))

Updated corner plot:

using CairoMakie, PairPlots
octocorner(model,chain,small=false,)