Fit Radial Velocity and Astrometry
You can use Octofitter to jointly fit relative astrometry data and radial velocity data. Below is an example. For more information on these functions, see previous guides.
Import required packages
using Octofitter
using OctofitterRadialVelocity
using CairoMakie
using PairPlots
using Distributions
using PlanetOrbitsWe now use PlanetOrbits.jl to create sample data. We start with a template orbit and record it's positon and velocity at a few epochs.
orb_template = orbit(
a = 1.0,
e = 0.7,
i= pi/4,
Ω = 0.1,
ω = 1π/4,
M = 1.0,
plx=100.0,
m =0,
tp =58829-40
)
Makie.lines(orb_template,axis=(;autolimitaspect=1))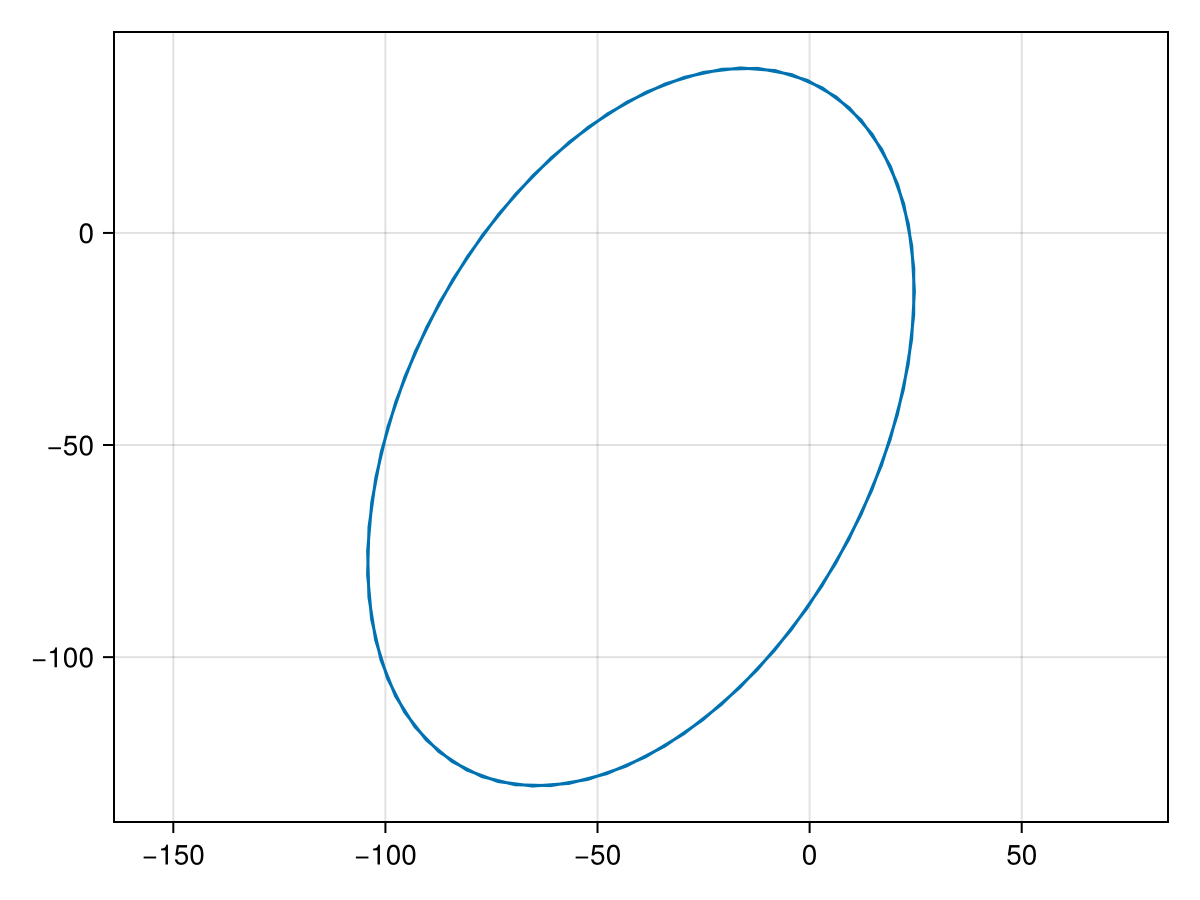
Sample position and store as relative astrometry measurements:
epochs = [58849,58852,58858,58890]
astrom_dat = Table(
epoch=epochs,
ra=raoff.(orb_template, epochs),
dec=decoff.(orb_template, epochs),
σ_ra=fill(1.0, size(epochs)),
σ_dec=fill(1.0, size(epochs)),
cor=fill(0.0, size(epochs))
)
astrom = PlanetRelAstromLikelihood(
astrom_dat,
name = "simulated",
variables = @variables begin
# Fixed values for this example - could be free variables:
jitter = 0 # mas [could use: jitter ~ Uniform(0, 10)]
northangle = 0 # radians [could use: northangle ~ Normal(0, deg2rad(1))]
platescale = 1 # relative [could use: platescale ~ truncated(Normal(1, 0.01), lower=0)]
end
)PlanetRelAstromLikelihood Table with 6 columns and 4 rows:
epoch ra dec σ_ra σ_dec cor
┌────────────────────────────────────────────
1 │ 58849 -18.3017 -108.907 1.0 1.0 0.0
2 │ 58852 -21.1181 -111.432 1.0 1.0 0.0
3 │ 58858 -26.6349 -115.889 1.0 1.0 0.0
4 │ 58890 -53.1334 -129.043 1.0 1.0 0.0And plot our simulated astrometry measurments:
fig = Makie.lines(orb_template,axis=(;autolimitaspect=1))
Makie.scatter!(astrom.table.ra, astrom.table.dec)
fig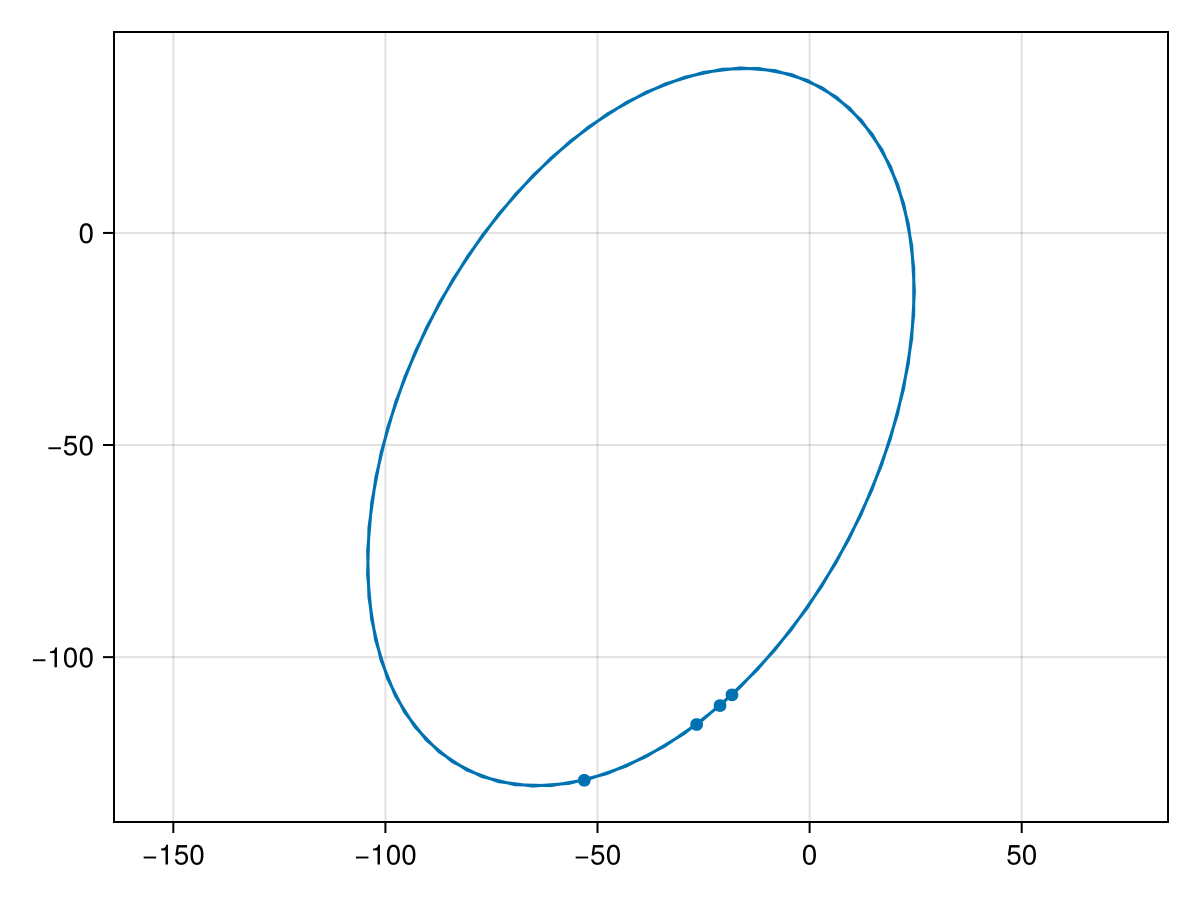
Generate a simulated RV curve from the same orbit:
using Random
Random.seed!(1)
epochs = 58849 .+ range(0,step=1.5, length=20)
planet_sim_mass = 0.001 # solar masses here
rvlike = MarginalizedStarAbsoluteRVLikelihood(
Table(
epoch=epochs,
rv=radvel.(orb_template, epochs, planet_sim_mass) .+ 150,
σ_rv=fill(5.0, size(epochs)),
),
name="inst1",
variables=@variables begin
jitter ~ LogUniform(0.1, 100) # m/s
end
)
epochs = 58949 .+ range(0,step=1.5, length=20)
rvlike2 = MarginalizedStarAbsoluteRVLikelihood(
Table(
epoch=epochs,
rv=radvel.(orb_template, epochs, planet_sim_mass) .- 150,
σ_rv=fill(5.0, size(epochs)),
),
name="inst2",
variables=@variables begin
jitter ~ LogUniform(0.1, 100) # m/s
end
)
fap = Makie.scatter(rvlike.table.epoch[:], rvlike.table.rv[:])
Makie.scatter!(rvlike2.table.epoch[:], rvlike2.table.rv[:])
fap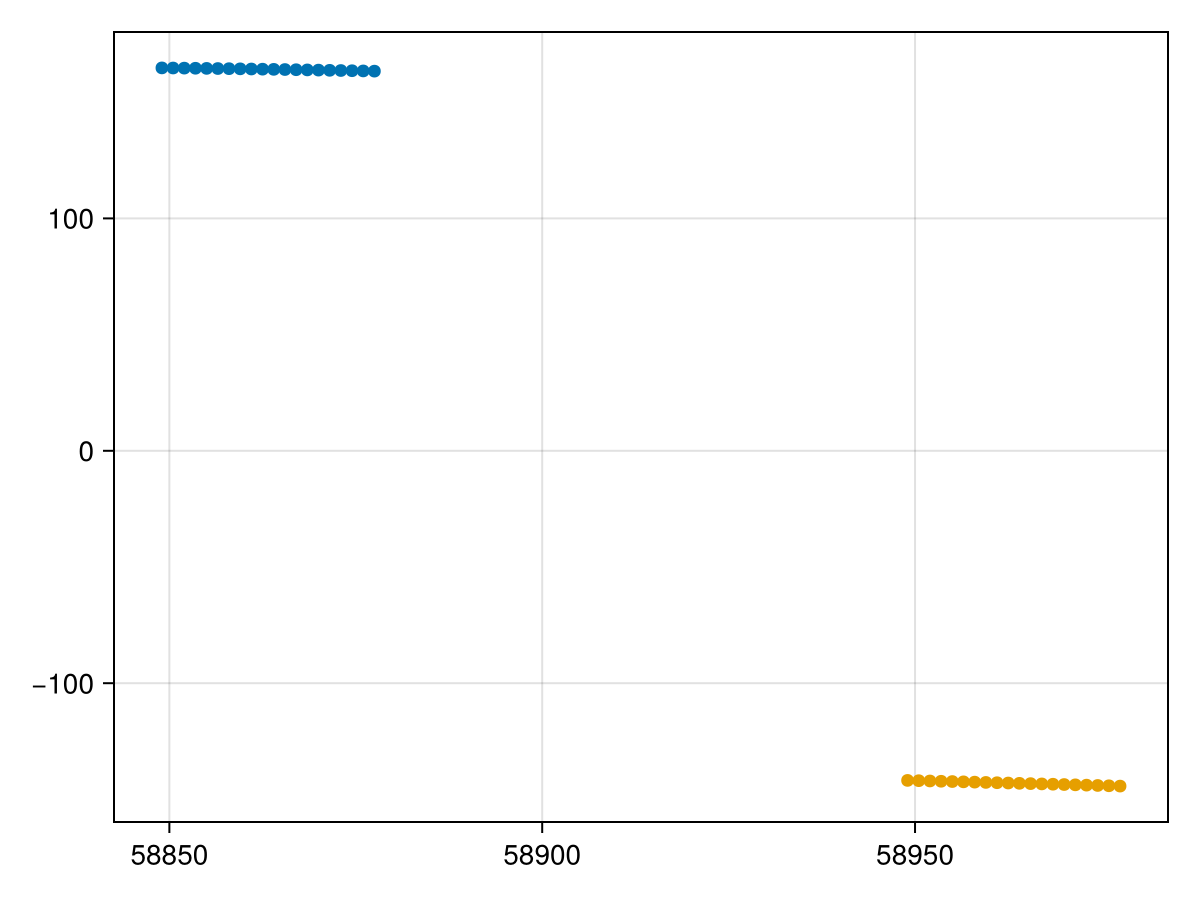
Now specify model and fit it:
planet_b = Planet(
name="b",
basis=Visual{KepOrbit},
likelihoods=[astrom],
variables=@variables begin
e ~ Uniform(0,0.999999)
a ~ truncated(Normal(1, 1),lower=0.1)
mass ~ truncated(Normal(1, 1), lower=0.)
i ~ Sine()
M = system.M
Ω ~ UniformCircular()
ω ~ UniformCircular()
θ ~ UniformCircular()
tp = θ_at_epoch_to_tperi(θ, 58849.0; M, e, a, i, ω, Ω) # reference epoch for θ. Choose an MJD date near your data.
end
)
sys = System(
name="test",
companions=[planet_b],
likelihoods=[rvlike, rvlike2],
variables=@variables begin
M ~ truncated(Normal(1, 0.04),lower=0.1) # (Baines & Armstrong 2011).
plx = 100.0
end
)
model = Octofitter.LogDensityModel(sys)
using Random
rng = Xoshiro(0) # seed the random number generator for reproducible results
results = octofit(rng, model, max_depth=9, adaptation=300, iterations=400)Chains MCMC chain (400×35×1 Array{Float64, 3}):
Iterations = 1:1:400
Number of chains = 1
Samples per chain = 400
Wall duration = 9.56 seconds
Compute duration = 9.56 seconds
parameters = M, plx, inst1_jitter, inst2_jitter, b_e, b_a, b_mass, b_i, b_Ωx, b_Ωy, b_ωx, b_ωy, b_θx, b_θy, b_Ω, b_ω, b_θ, b_M, b_tp, b_simulated_jitter, b_simulated_northangle, b_simulated_platescale
internals = n_steps, is_accept, acceptance_rate, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size, is_adapt, loglike, logpost, tree_depth, numerical_error
Summary Statistics
parameters mean std mcse ess_bulk ess_tai ⋯
Symbol Float64 Float64 Float64 Float64 Float6 ⋯
M 0.9935 0.0396 0.0023 303.3639 332.300 ⋯
plx 100.0000 0.0000 NaN NaN Na ⋯
inst1_jitter 0.4041 0.3603 0.0288 18.0586 83.278 ⋯
inst2_jitter 0.4306 0.3600 0.0241 142.1659 104.326 ⋯
b_e 0.6289 0.2159 0.1283 2.3420 21.246 ⋯
b_a 1.1162 0.3875 0.2396 2.0286 12.127 ⋯
b_mass 0.8933 0.6518 0.2881 4.6885 136.517 ⋯
b_i 0.7286 0.3097 0.2283 2.0373 13.220 ⋯
b_Ωx 0.8583 0.2269 0.0788 12.1858 29.257 ⋯
b_Ωy 0.2456 0.4350 0.2905 2.3086 23.715 ⋯
b_ωx 0.7385 0.2376 0.0393 39.1134 83.121 ⋯
b_ωy 0.3729 0.5351 0.2605 7.1168 35.575 ⋯
b_θx -0.9931 0.1072 0.0073 287.7154 219.823 ⋯
b_θy -0.1670 0.0181 0.0011 281.8338 133.585 ⋯
b_Ω 0.2839 0.5054 0.3388 2.2743 25.457 ⋯
b_ω 0.4434 0.6215 0.2933 5.8287 63.046 ⋯
b_θ -2.9749 0.0067 0.0005 195.1887 105.293 ⋯
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱
3 columns and 5 rows omitted
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% ⋯
Symbol Float64 Float64 Float64 Float64 ⋯
M 0.9150 0.9660 0.9953 1.0214 ⋯
plx 100.0000 100.0000 100.0000 100.0000 ⋯
inst1_jitter 0.1052 0.1548 0.2616 0.5221 ⋯
inst2_jitter 0.1092 0.1776 0.3010 0.5712 ⋯
b_e 0.0852 0.5107 0.7297 0.7885 ⋯
b_a 0.8138 0.8604 0.9860 1.2231 ⋯
b_mass 0.0658 0.4011 0.7244 1.2659 ⋯
b_i 0.2505 0.4328 0.7645 0.9957 ⋯
b_Ωx 0.2484 0.7622 0.9011 1.0020 ⋯
b_Ωy -0.5546 -0.0712 0.2669 0.5677 ⋯
b_ωx 0.2807 0.5506 0.7987 0.9142 ⋯
b_ωy -0.7807 0.0176 0.5255 0.8233 ⋯
b_θx -1.2101 -1.0602 -0.9856 -0.9239 ⋯
b_θy -0.2063 -0.1786 -0.1660 -0.1554 ⋯
b_Ω -0.6399 -0.0668 0.2713 0.5869 ⋯
b_ω -0.7637 0.0162 0.5626 0.9751 ⋯
b_θ -2.9882 -2.9796 -2.9750 -2.9702 ⋯
⋮ ⋮ ⋮ ⋮ ⋮ ⋱
1 column and 5 rows omitted
Display results as a corner plot:
octocorner(model,results, small=true)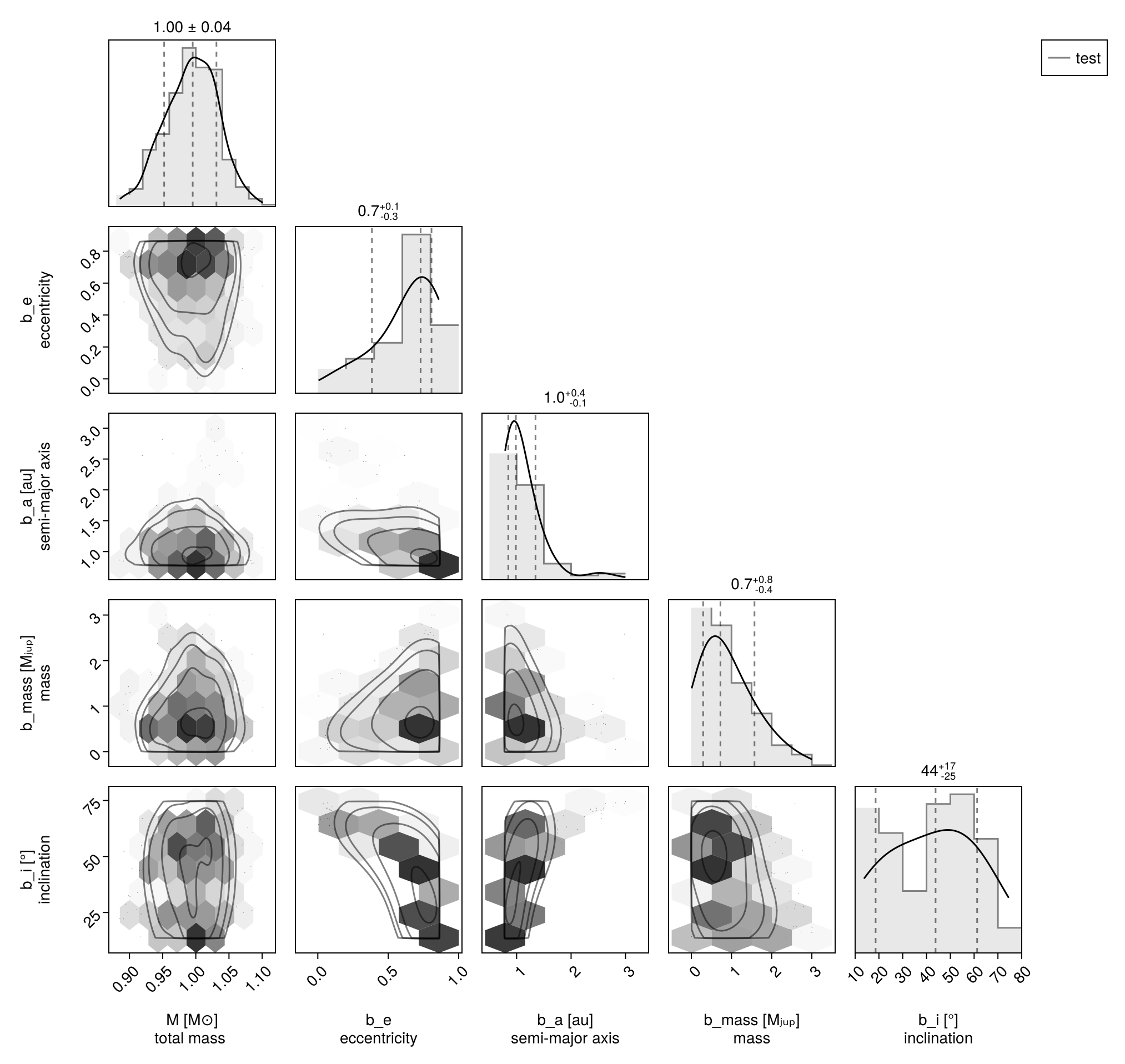
Plot RV curve, phase folded curve, and binned residuals:
Octofitter.rvpostplot(model, results)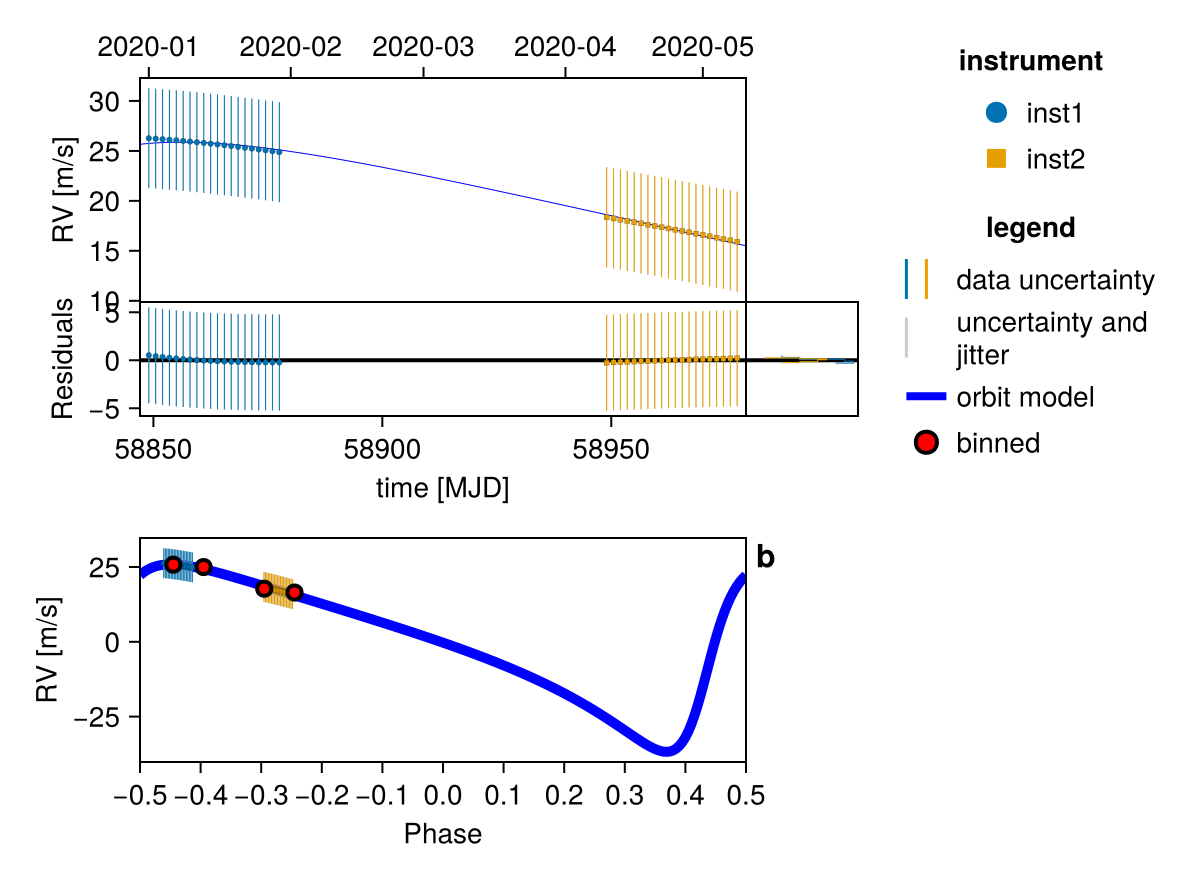
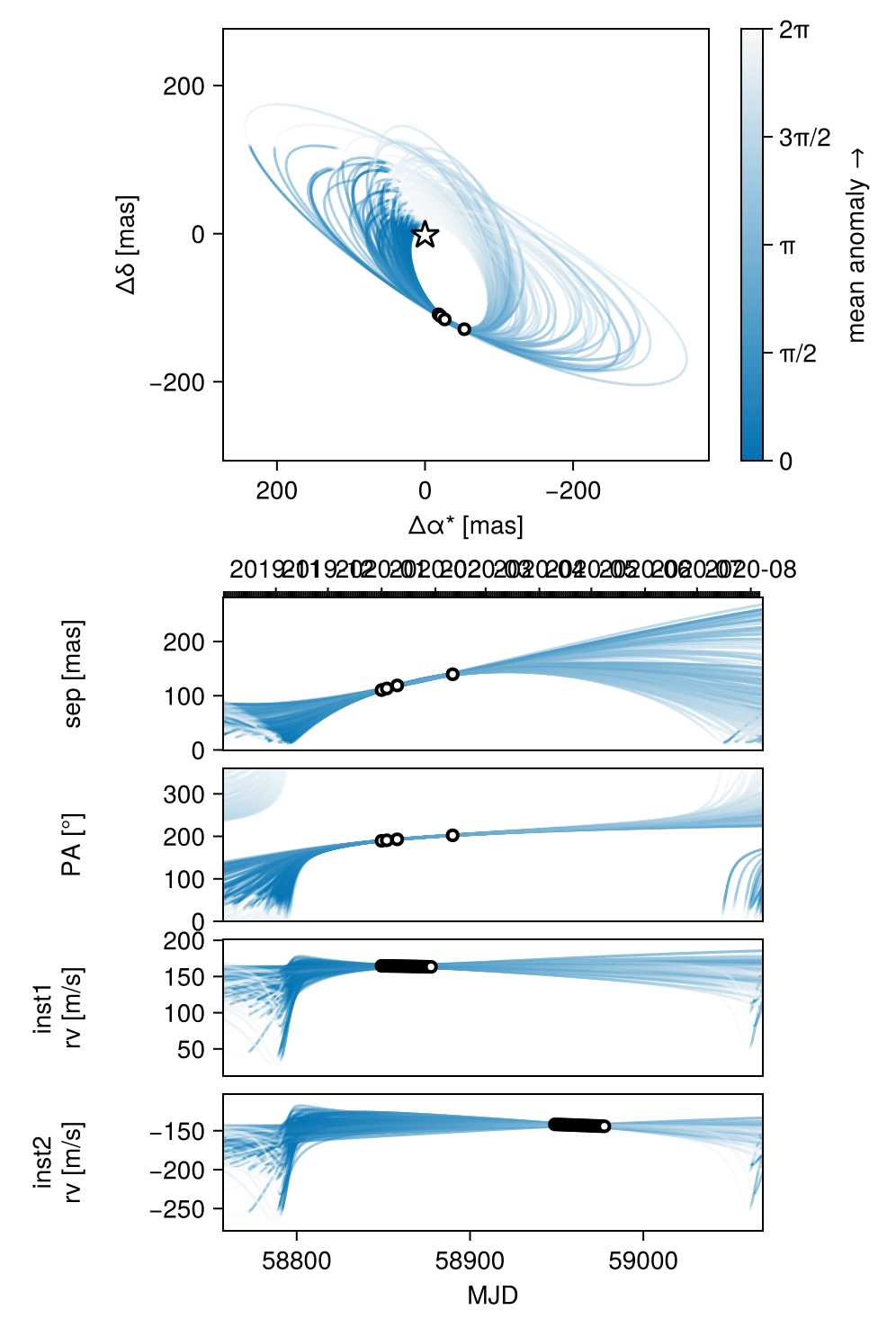
Display RV, PMA, astrometry, relative separation, position angle, and 3D projected views:
octoplot(model, results)