Fit Relative RV Data
Octofitter includes support for fitting relative radial velocity data. Currently this is only tested with a single companion. Please open an issue if you would like to fit multiple companions simultaneously.
The convention we adopt is that positive relative radial velocity is the velocity of the companion (exoplanets) minus the velocity of the host (star).
To fit relative RV data, start by creating a likelihood object:
using Octofitter
using OctofitterRadialVelocity
using CairoMakie
using Distributions
rv_dat_1 = Table(
epoch=55000:100:57400,
rv = [
-24022.74
-18571.33
14221.56
26076.89
-459.26
-26319.26
-13430.96
19230.96
23580.26
-6786.28
-27161.78
-7548.58
23177.95
19780.94
-12738.39
-26503.74
-1249.19
25844.47
14888.83
-17986.76
-24381.49
5119.22
27083.2
9174.18
-22241.45
],
# Hint! Type as \sigma + <TAB>
σ_rv= fill(15000.0, 25),
)
rel_rv_like = PlanetRelativeRVLikelihood(
rv_dat_1,
name="simulated data",
variables = @variables begin
jitter ~ LogUniform(0.1, 1000) # m/s
end
)PlanetRelativeRVLikelihood Table with 3 columns and 25 rows:
epoch rv σ_rv
┌─────────────────────────
1 │ 55000 -24022.7 15000.0
2 │ 55100 -18571.3 15000.0
3 │ 55200 14221.6 15000.0
4 │ 55300 26076.9 15000.0
5 │ 55400 -459.26 15000.0
6 │ 55500 -26319.3 15000.0
7 │ 55600 -13431.0 15000.0
8 │ 55700 19231.0 15000.0
9 │ 55800 23580.3 15000.0
10 │ 55900 -6786.28 15000.0
11 │ 56000 -27161.8 15000.0
12 │ 56100 -7548.58 15000.0
13 │ 56200 23178.0 15000.0
14 │ 56300 19780.9 15000.0
15 │ 56400 -12738.4 15000.0
16 │ 56500 -26503.7 15000.0
17 │ 56600 -1249.19 15000.0
⋮ │ ⋮ ⋮ ⋮See the standard radial velocity tutorial for examples on how this data can be loaded from a CSV file.
The relative RV likelihood does not incorporate an instrument-specific RV offset. A jitter parameter can still be specified in the likelihood's @variables block, as can parameters for a gaussian process model of stellar noise. Currently only a single instrument jitter parameter is supported. If you need to model relative radial velocities from multiple instruments with different jitters, please open an issue on GitHub.
Next, create a planet and system model, attaching the relative rv likelihood to the planet.
planet_1 = Planet(
name="b",
basis=RadialVelocityOrbit,
likelihoods=[rel_rv_like],
variables=@variables begin
M ~ truncated(Normal(1.2, 0.1), lower=0.1) # total mass in solar masses
a ~ Uniform(0,10)
e ~ Uniform(0.0, 0.5)
i ~ Sine()
ω ~ Uniform(0, 2pi)
Ω ~ Uniform(0, 2pi)
τ ~ Uniform(0, 1.0)
P = √(a^3/M)
tp = τ*P*365.25 + 60000 # reference epoch for τ. Choose an MJD date near your data.
end
)
sys = System(
name = "Example-System",
companions=[planet_1],
likelihoods=[],
variables=@variables begin
end
)
model = Octofitter.LogDensityModel(sys)LogDensityModel for System Example-System of dimension 8 and 25 epochs with fields .ℓπcallback and .∇ℓπcallback
Initialize the model and verify starting point
init_chain = initialize!(model)
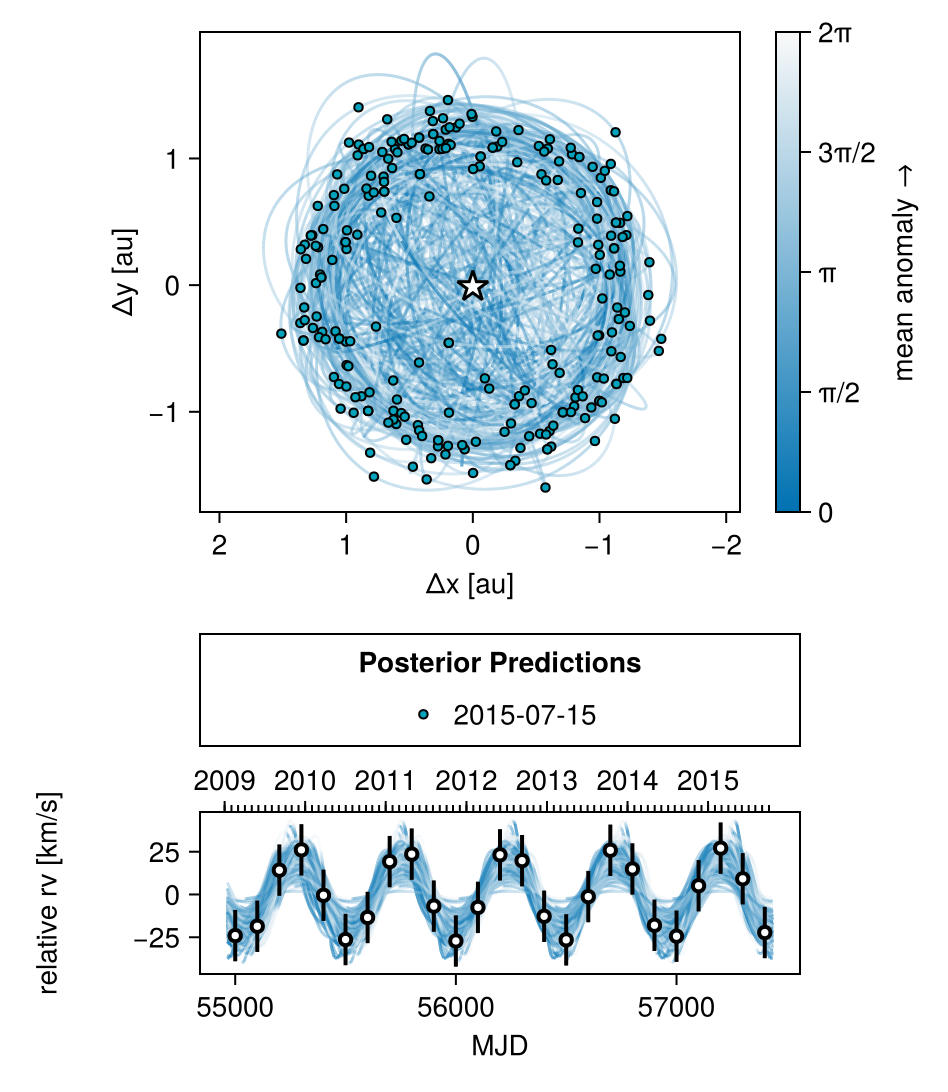
octoplot(model, init_chain)
using Random
rng = Random.Xoshiro(123)
chain = octofit(rng, model)Chains MCMC chain (1000×23×1 Array{Float64, 3}):
Iterations = 1:1:1000
Number of chains = 1
Samples per chain = 1000
Wall duration = 1.29 seconds
Compute duration = 1.29 seconds
parameters = b_M, b_a, b_e, b_i, b_ω, b_Ω, b_τ, b_P, b_tp, b_simulated_data_jitter
internals = n_steps, is_accept, acceptance_rate, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size, is_adapt, loglike, logpost, tree_depth, numerical_error
Summary Statistics
parameters mean std mcse ess_bulk ess_ ⋯
Symbol Float64 Float64 Float64 Float64 Flo ⋯
b_M 1.1909 0.0943 0.0037 658.8695 464. ⋯
b_a 1.2733 0.0373 0.0017 511.5274 528. ⋯
b_e 0.1230 0.0958 0.0035 675.3891 363. ⋯
b_i 1.5572 0.6764 0.0231 860.9770 676. ⋯
b_ω 2.6080 1.5833 0.0687 491.3326 351. ⋯
b_Ω 3.1460 1.8494 0.0502 1381.8426 569. ⋯
b_τ 0.6059 0.2474 0.0101 557.9129 540. ⋯
b_P 1.3180 0.0218 0.0009 588.9291 432. ⋯
b_tp 60292.1324 119.8290 4.8772 564.9357 495. ⋯
b_simulated_data_jitter 99.6248 191.4899 6.3200 987.2941 760. ⋯
3 columns omitted
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% ⋯
Symbol Float64 Float64 Float64 Float64 ⋯
b_M 1.0058 1.1305 1.1907 1.2552 ⋯
b_a 1.1988 1.2488 1.2732 1.2993 ⋯
b_e 0.0030 0.0483 0.1041 0.1733 ⋯
b_i 0.3899 1.0382 1.5516 2.0632 ⋯
b_ω 0.0938 1.2198 2.5363 3.8649 ⋯
b_Ω 0.1754 1.5060 3.1311 4.7767 ⋯
b_τ 0.1355 0.4089 0.6139 0.8229 ⋯
b_P 1.2782 1.3032 1.3176 1.3327 ⋯
b_tp 60064.1822 60196.1475 60296.1756 60396.7878 ⋯
b_simulated_data_jitter 0.1437 1.0496 9.7640 89.5023 ⋯
1 column omitted
octoplot(model, chain, show_physical_orbit=true, mark_epochs_mjd=[mjd("2015-07-15")])