Basic RV Fit
You can use Octofitter to fit radial velocity data, either alone or in combination with other kinds of data. Multiple instruments (any number) are supported, as are arbitrary trends, and gaussian processes to model stellar activity.
Radial velocity modelling is supported in Octofitter via the extension package OctofitterRadialVelocity. To install it, run pkg> add OctofitterRadialVelocity
For this example, we will fit the orbit of the planet K2-131, and reproduce this RadVel tutorial.
We will use the following packages:
using Octofitter
using OctofitterRadialVelocity
using PlanetOrbits
using CairoMakie
using PairPlots
using CSV
using DataFrames
using DistributionsWe will start by downloading and preparing a table of radial velocity measurements, and create a StarAbsoluteRVLikelihood object to hold them.
The following functions allow you to directly load data from various public RV databases:
HARPS_DR1_rvs("star-name")HARPS_RVBank_observations("star-name")Lick_rvs("star-name")HIRES_rvs("star-name")
Make sure to credit the sources using the citation printed when you first access the catalog. Calling those functions with the name of a star will return a StarAbsoluteRVLikelihood table.
If you would like to manually specify RV data, use the following format:
rv_data = Table(
# epoch is in units of MJD. `jd2mjd` is a helper function to convert.
# you can also put `years2mjd(2016.1231)`.
# rv and σ_rv are in units of meters/second
epoch=jd2mjd.([2455110.97985, 2455171.90825]),
rv=[-6.54, -3.33],
σ_rv=[1.30, 1.09]
)
rv_like = StarAbsoluteRVLikelihood(rv_data,
name="insert name here",
variables=@variables begin
offset ~ Uniform(-1000, 1000) # m/s
jitter ~ LogUniform(0.01, 10) # m/s
end
)Basic Fit
For this example, to replicate the results of RadVel, we will download their example data for K2-131 and format it for Octofitter:
rv_file = download("https://raw.githubusercontent.com/California-Planet-Search/radvel/master/example_data/k2-131.txt")
rv_dat_raw = CSV.read(rv_file, DataFrame, delim=' ')
rv_dat = DataFrame();
rv_dat.epoch = jd2mjd.(rv_dat_raw.time)
rv_dat.rv = rv_dat_raw.mnvel
rv_dat.σ_rv = rv_dat_raw.errvel
tels = sort(unique(rv_dat_raw.tel))
# This table includes data from two insturments. We create a separate
# likelihood object for each:
rvlike_harps = StarAbsoluteRVLikelihood(
rv_dat[rv_dat_raw.tel .== "harps-n",:],
name="harps-n",
variables=@variables begin
offset ~ Normal(-6693,100) # m/s
jitter ~ LogUniform(0.1,100) # m/s
end
)
rvlike_pfs = StarAbsoluteRVLikelihood(
rv_dat[rv_dat_raw.tel .== "pfs",:],
name="pfs",
variables=@variables begin
offset ~ Normal(0,100) # m/s
jitter ~ LogUniform(0.1,100) # m/s
end
)StarAbsoluteRVLikelihood Table with 3 columns and 31 rows:
epoch rv σ_rv
┌──────────────────────
1 │ 57828.4 -45.17 3.88
2 │ 57828.4 -36.47 4.03
3 │ 57829.2 -20.52 3.55
4 │ 57829.2 -4.58 6.07
5 │ 57830.1 17.71 3.56
6 │ 57830.1 23.34 3.48
7 │ 57830.2 21.34 3.51
8 │ 57830.2 19.92 3.26
9 │ 57830.2 -0.74 3.44
10 │ 57830.3 16.9 3.5
11 │ 57830.3 8.25 4.64
12 │ 57830.4 -4.06 4.91
13 │ 57832.1 -29.51 4.96
14 │ 57832.1 -21.56 4.11
15 │ 57832.2 -25.76 5.59
16 │ 57833.1 2.1 3.91
17 │ 57833.1 4.38 3.73
⋮ │ ⋮ ⋮ ⋮Now, create a planet. We can use the RadialVelocityOrbit type from PlanetOrbits.jl that requires fewer parameters (eg no inclination or longitude of ascending node). We could instead use a Visual{KepOrbit} or similar if we wanted to include these parameters and visualize the orbit in the plane of the sky.
planet_1 = Planet(
name="b",
basis=RadialVelocityOrbit,
likelihoods=[],
variables=@variables begin
e = 0
ω = 0.0
# To match RadVel, we set a prior on Period and calculate semi-major axis from it
P ~ truncated(
Normal(0.3693038/365.256360417, 0.0000091/365.256360417),
lower=0.0001
)
M = system.M
a = cbrt(M * P^2) # note the equals sign.
τ ~ UniformCircular(1.0)
tp = τ*P*365.256360417 + 57782 # reference epoch for τ. Choose an MJD date near your data.
# minimum planet mass [jupiter masses]. really m*sin(i)
mass ~ LogUniform(0.001, 10)
end
)
sys = System(
name = "k2_132",
companions=[planet_1],
likelihoods=[rvlike_harps, rvlike_pfs],
variables=@variables begin
M ~ truncated(Normal(0.82, 0.02),lower=0.1) # (Baines & Armstrong 2011).
end
)System model k2_132
Derived:
Priors:
M Truncated(Distributions.Normal{Float64}(μ=0.82, σ=0.02); lower=0.1)
Planet b
Derived:
τ, e, ω, M, a, tp,
Priors:
P Truncated(Distributions.Normal{Float64}(μ=0.001011081092683449, σ=2.4914008313533153e-8); lower=0.0001)
τx Distributions.Normal{Float64}(μ=0.0, σ=1.0)
τy Distributions.Normal{Float64}(μ=0.0, σ=1.0)
mass Distributions.LogUniform{Float64}(a=0.001, b=10.0)
Octofitter.UnitLengthPrior{:τx, :τy}: √(τx^2+τy^2) ~ LogNormal(log(1), 0.02)
StarAbsoluteRVLikelihood Table with 3 columns and 39 rows:
epoch rv σ_rv
┌─────────────────────────
1 │ 57782.2 -6682.78 3.71
2 │ 57783.1 -6710.55 5.95
3 │ 57783.2 -6698.96 8.76
4 │ 57812.1 -6672.32 4.0
5 │ 57812.2 -6672.0 4.22
6 │ 57812.2 -6690.31 4.63
7 │ 57813.0 -6701.27 4.12
8 │ 57813.1 -6700.71 5.34
9 │ 57813.1 -6695.97 3.67
10 │ 57813.1 -6705.87 4.23
11 │ 57813.1 -6694.27 5.12
12 │ 57813.2 -6699.99 5.0
13 │ 57813.2 -6696.17 10.43
14 │ 57836.0 -6675.4 7.03
15 │ 57836.0 -6665.92 7.48
16 │ 57836.0 -6661.9 6.03
17 │ 57836.1 -6657.92 5.08
⋮ │ ⋮ ⋮ ⋮StarAbsoluteRVLikelihood Table with 3 columns and 31 rows:
epoch rv σ_rv
┌──────────────────────
1 │ 57828.4 -45.17 3.88
2 │ 57828.4 -36.47 4.03
3 │ 57829.2 -20.52 3.55
4 │ 57829.2 -4.58 6.07
5 │ 57830.1 17.71 3.56
6 │ 57830.1 23.34 3.48
7 │ 57830.2 21.34 3.51
8 │ 57830.2 19.92 3.26
9 │ 57830.2 -0.74 3.44
10 │ 57830.3 16.9 3.5
11 │ 57830.3 8.25 4.64
12 │ 57830.4 -4.06 4.91
13 │ 57832.1 -29.51 4.96
14 │ 57832.1 -21.56 4.11
15 │ 57832.2 -25.76 5.59
16 │ 57833.1 2.1 3.91
17 │ 57833.1 4.38 3.73
⋮ │ ⋮ ⋮ ⋮
Note how the rvlike object was attached to the k2_132 system instead of the planet. This is because the observed radial velocity is of the star, and is caused by any/all orbiting planets.
The rv0 and jitter parameters specify priors for the instrument-specific offset and white noise jitter standard deviation. The _i index matches the inst_idx used to create the observation table.
Note also here that the mass variable is really msini, or the minimum mass of the planet.
We can now prepare our model for sampling.
model = Octofitter.LogDensityModel(sys)LogDensityModel for System k2_132 of dimension 9 and 71 epochs with fields .ℓπcallback and .∇ℓπcallback
Initialize the starting points, and confirm the data are entered correcly:
init_chain = initialize!(model)
using CairoMakie
fig = Octofitter.rvpostplot(model, init_chain)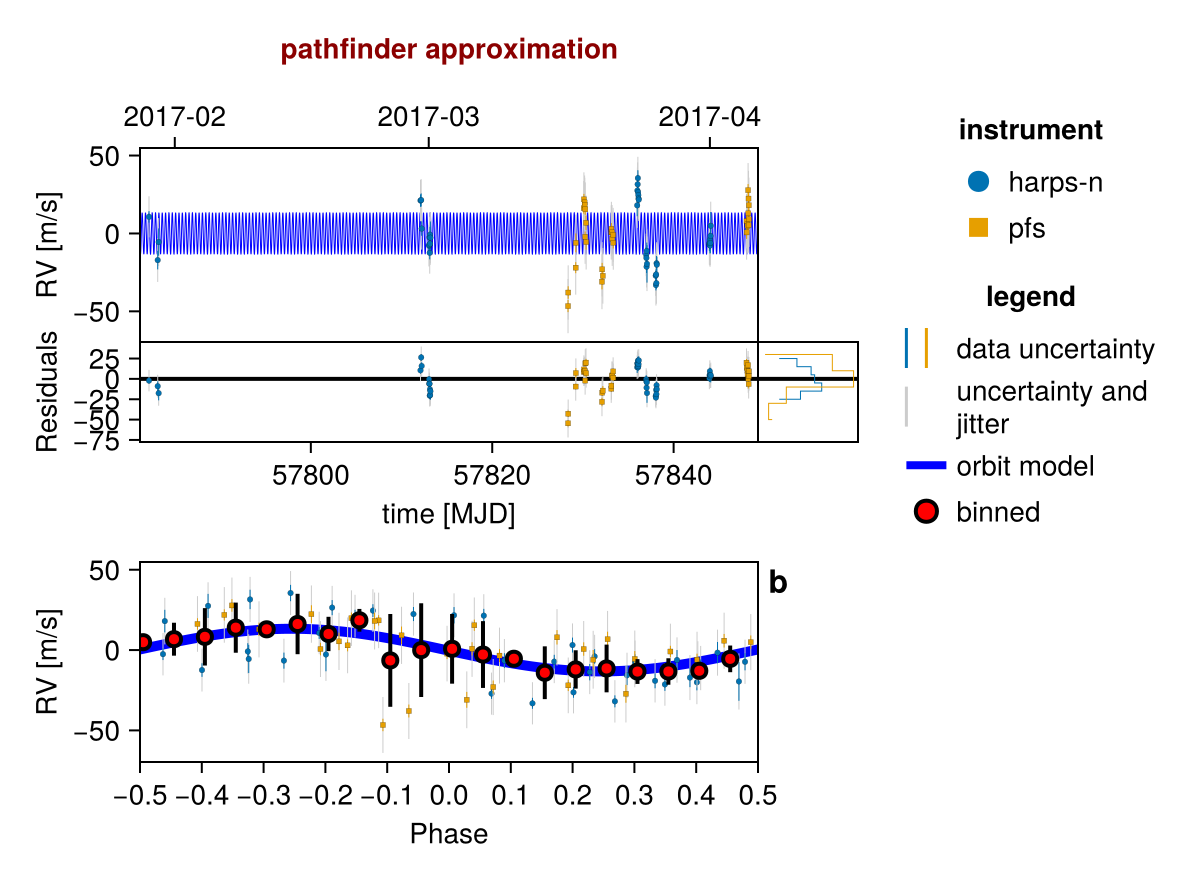
Sample:
using Random
rng = Random.Xoshiro(0)
chain = octofit(rng, model)Chains MCMC chain (1000×28×1 Array{Float64, 3}):
Iterations = 1:1:1000
Number of chains = 1
Samples per chain = 1000
Wall duration = 19.36 seconds
Compute duration = 19.36 seconds
parameters = M, harps_n_offset, harps_n_jitter, pfs_offset, pfs_jitter, b_P, b_τx, b_τy, b_mass, b_τ, b_e, b_ω, b_M, b_a, b_tp
internals = n_steps, is_accept, acceptance_rate, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size, is_adapt, loglike, logpost, tree_depth, numerical_error
Summary Statistics
parameters mean std mcse ess_bulk ess_tail r ⋯
Symbol Float64 Float64 Float64 Float64 Float64 Floa ⋯
M 0.8197 0.0197 0.0006 936.9058 659.8062 0.9 ⋯
harps_n_offset -6693.7329 2.5414 0.0849 901.3477 553.0357 0.9 ⋯
harps_n_jitter 13.8722 2.0104 0.0682 924.2135 741.0364 1.0 ⋯
pfs_offset 1.3951 3.2844 0.1073 934.2355 645.1686 1.0 ⋯
pfs_jitter 17.6387 2.6338 0.0999 782.1500 550.1379 1.0 ⋯
b_P 0.0010 0.0000 0.0000 930.2032 679.6304 1.0 ⋯
b_τx 0.7237 0.1747 0.0065 776.4507 607.3337 0.9 ⋯
b_τy -0.6520 0.1910 0.0070 832.5154 549.9624 0.9 ⋯
b_mass 0.0420 0.0078 0.0003 734.8539 415.7334 1.0 ⋯
b_τ -0.1166 0.0382 0.0015 676.0917 564.5600 0.9 ⋯
b_e 0.0000 0.0000 NaN NaN NaN ⋯
b_ω 0.0000 0.0000 NaN NaN NaN ⋯
b_M 0.8197 0.0197 0.0006 936.9058 659.8062 0.9 ⋯
b_a 0.0094 0.0001 0.0000 938.5972 659.8062 0.9 ⋯
b_tp 57781.9570 0.0141 0.0006 676.0970 564.5600 0.9 ⋯
2 columns omitted
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97 ⋯
Symbol Float64 Float64 Float64 Float64 Floa ⋯
M 0.7842 0.8054 0.8192 0.8340 0.8 ⋯
harps_n_offset -6698.7667 -6695.5128 -6693.7173 -6692.0106 -6688.8 ⋯
harps_n_jitter 10.4359 12.4501 13.6372 15.1790 18.3 ⋯
pfs_offset -5.1914 -0.7373 1.3512 3.5156 7.8 ⋯
pfs_jitter 13.3827 15.7606 17.3678 19.1364 23.8 ⋯
b_P 0.0010 0.0010 0.0010 0.0010 0.0 ⋯
b_τx 0.3475 0.6229 0.7373 0.8428 1.0 ⋯
b_τy -0.9986 -0.7847 -0.6565 -0.5265 -0.2 ⋯
b_mass 0.0265 0.0369 0.0418 0.0474 0.0 ⋯
b_τ -0.1924 -0.1415 -0.1161 -0.0912 -0.0 ⋯
b_e 0.0000 0.0000 0.0000 0.0000 0.0 ⋯
b_ω 0.0000 0.0000 0.0000 0.0000 0.0 ⋯
b_M 0.7842 0.8054 0.8192 0.8340 0.8 ⋯
b_a 0.0093 0.0094 0.0094 0.0095 0.0 ⋯
b_tp 57781.9289 57781.9477 57781.9571 57781.9663 57781.9 ⋯
1 column omitted
Excellent! Let's plot an orbit sampled from the posterior:
using CairoMakie
fig = Octofitter.rvpostplot(model, chain) # saved to "k2_132-rvpostplot.png"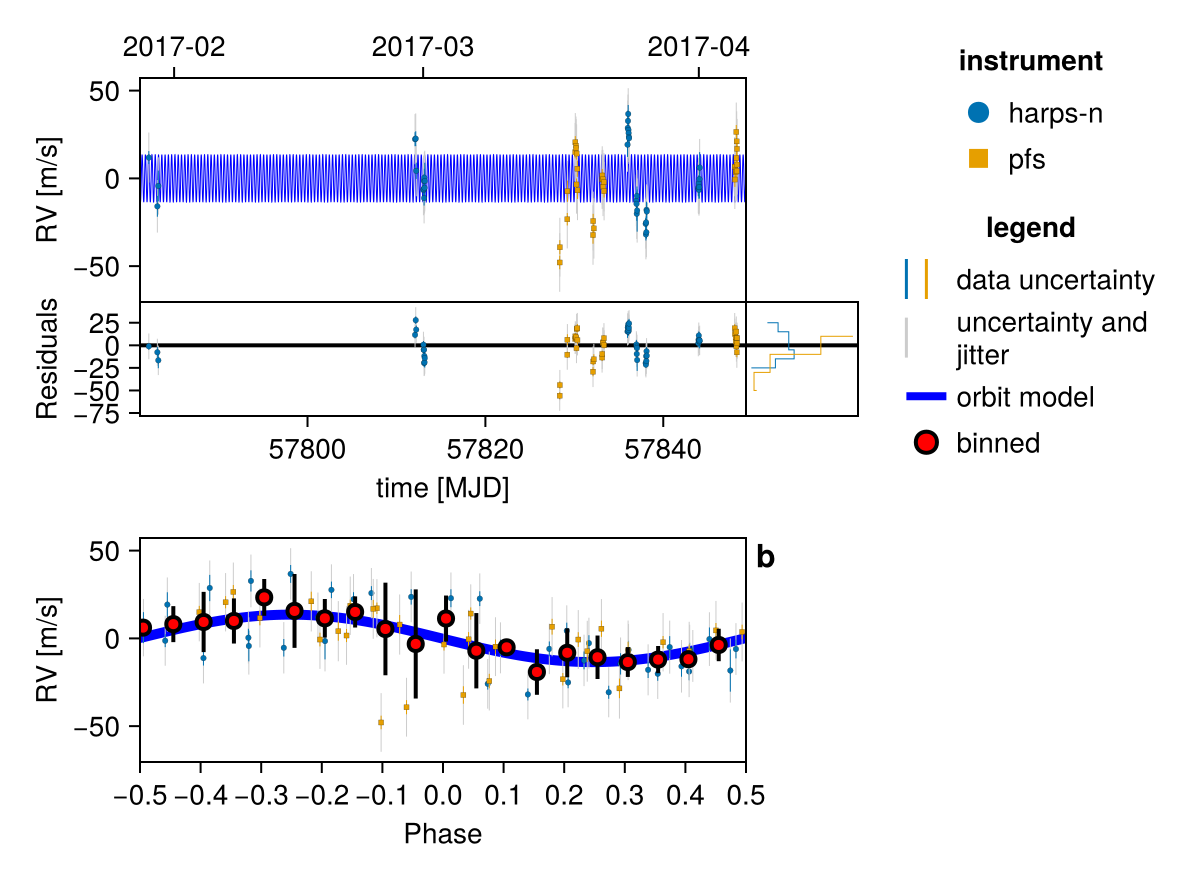
We can also plot a sample of draws from the posterior:
using CairoMakie: Makie
octoplot(model, chain)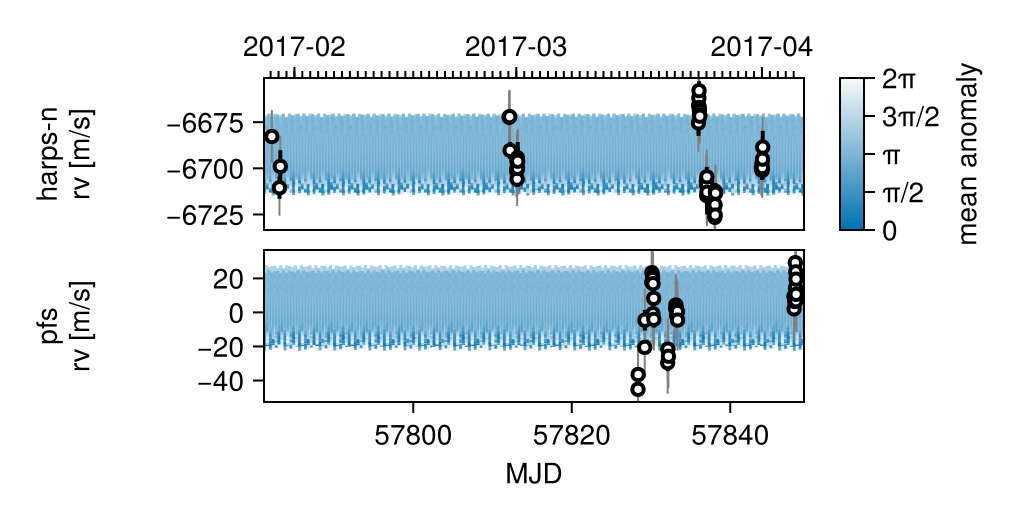
And create a corner plot:
using PairPlots, CairoMakie
octocorner(model, chain)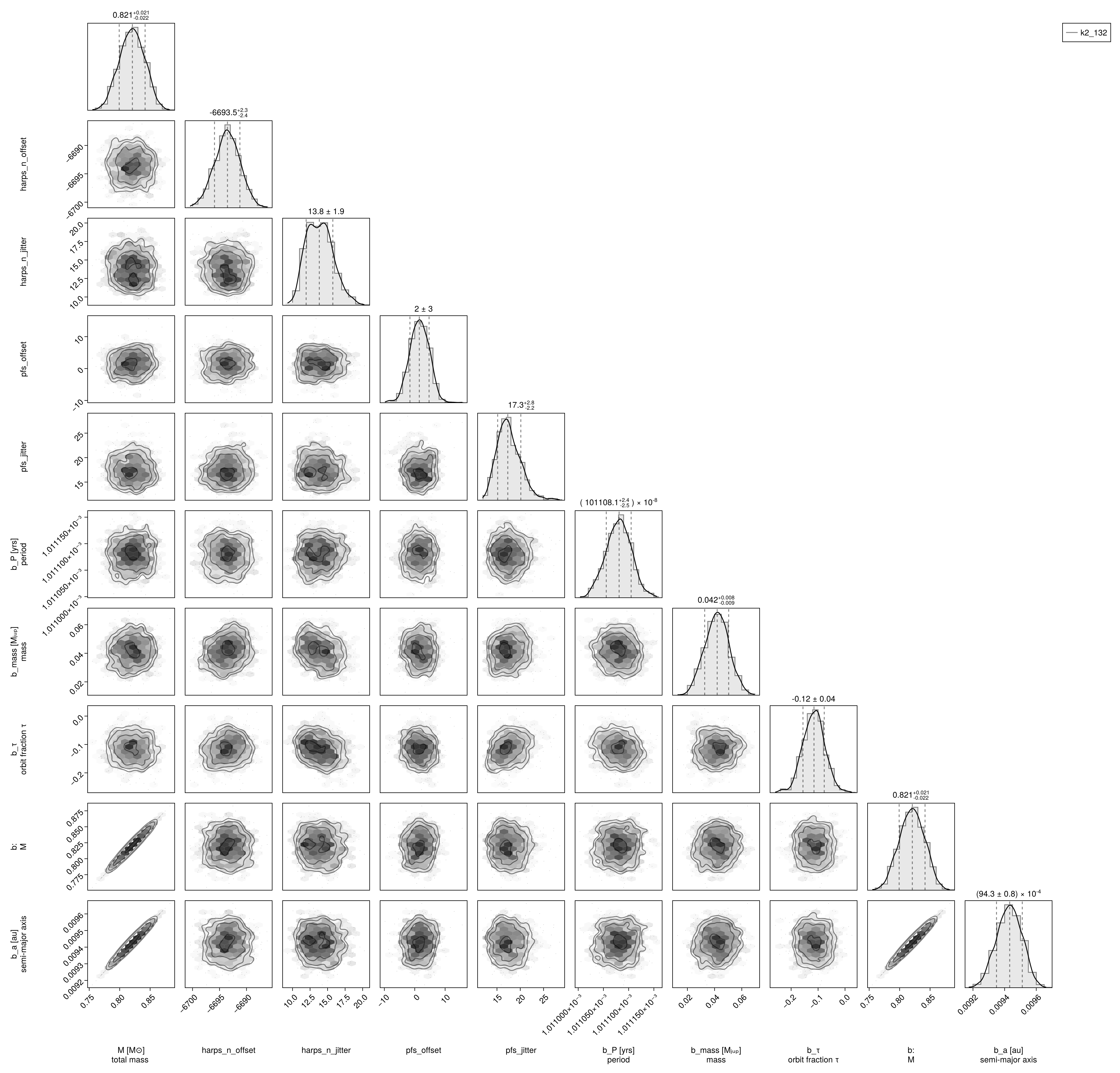
This example continues in Fit Gaussian Process.