Kepler Solvers
The heart of this package is being able to take a set of Keplerian elements and output relative positions, velocities, etc.
This normaly requires solving Kepler's equation numerically. This package supports a multitude of solver algorithms that can be passed to orbitsolve:
The last of these RootsMethod, allows one to substitute any algorithm from the Roots.jl package. These include many different classical and modern root finding algorithms.chosen precision, including artibrary precision BigFloats. Using big floats with, for example, Roots.PlanetOrbits.Thukral5B and a tight tolerenace, allows you to solve orbits up to arbitrary precision.
The default choice is Auto, which currently selects Markley for all cases. The Markley algorithm is very fast, reasonably accurate, and always converges, making it a good default choice.
The Markley algorithm is a tweaked version of the algorithm from AstroLib.jl. It is non-iterative and converges with less than 1e-15 relative error across the full range of e between 0 and 1. On my laptop, this solves for a single eccentric anomaly in just 71 ns. Since it is implemented in pure Julia, there is no overhead from calling into a C or Cython compiled function and no need for vectorization.
Examples
using PlanetOrbits, BenchmarkTools
orb = orbit(a=1.2, e=0.1, M=1.0, ω=1.4, τ=0.5)
t = mjd("2025-06-23")
@benchmark orbitsolve(orb, t, PlanetOrbits.Markley())BenchmarkTools.Trial: 10000 samples with 616 evaluations per sample.
Range (min … max): 197.188 ns … 15.798 μs ┊ GC (min … max): 0.00% … 98.46%
Time (median): 198.196 ns ┊ GC (median): 0.00%
Time (mean ± σ): 212.684 ns ± 204.132 ns ┊ GC (mean ± σ): 3.24% ± 6.05%
█▆▂▂ ▃▃▁▁ ▁ ▁▁▁▁▂▁▁ ▁
█████▇▆▅▆▆▅▅████████▇▇██▇▆▆▅▅▄▅▅▄▄▄▁▆██████████▅▆▆▅▆▅▇▇▇▆▇▅▃▅ █
197 ns Histogram: log(frequency) by time 269 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.Goat())BenchmarkTools.Trial: 10000 samples with 145 evaluations per sample.
Range (min … max): 699.448 ns … 64.384 μs ┊ GC (min … max): 0.00% … 98.41%
Time (median): 753.897 ns ┊ GC (median): 0.00%
Time (mean ± σ): 761.842 ns ± 812.927 ns ┊ GC (mean ± σ): 1.49% ± 1.39%
▂▁ ▄▂ ▂█▂
▁▅██▅▂▁▁▁▁▁▁▁▁▁▁▁▁▁▄██▄▄███▄▂▂▃▂▁▂▃▃▂▁▁▁▁▁▁▁▂▂▂▁▂▂▂▂▁▁▁▁▁▁▁▁▁ ▂
699 ns Histogram: frequency by time 837 ns <
Memory estimate: 128 bytes, allocs estimate: 1.using Roots
@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.Newton()))BenchmarkTools.Trial: 10000 samples with 372 evaluations per sample.
Range (min … max): 252.110 ns … 23.904 μs ┊ GC (min … max): 0.00% … 98.32%
Time (median): 257.687 ns ┊ GC (median): 0.00%
Time (mean ± σ): 286.162 ns ± 342.554 ns ┊ GC (mean ± σ): 2.23% ± 2.28%
▆█▆▂ ▃▂▁ ▂▃▄▅▅▄▃▃▄▄▄▁ ▁▁▁ ▂
████▅▇█▆▅▄▄▄▅▅████▇▆▆▆▆▆▄▃████████████▇▆▆█▇████████▇▅▅▅▄▄▃▄▃▃ █
252 ns Histogram: log(frequency) by time 352 ns <
Memory estimate: 128 bytes, allocs estimate: 1.using Roots
@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.Thukral3B()))BenchmarkTools.Trial: 10000 samples with 282 evaluations per sample.
Range (min … max): 288.128 ns … 33.518 μs ┊ GC (min … max): 0.00% … 98.61%
Time (median): 336.447 ns ┊ GC (median): 0.00%
Time (mean ± σ): 335.336 ns ± 560.279 ns ┊ GC (mean ± σ): 3.25% ± 1.97%
▆█▆▃ ▁▂▂ ▂▃▃▆▇▇▅▃▂▁▄▅▅▃ ▁▂▂▁ ▂
████▇▆▇▇▆▆▅▃▅▄▂▂▂▂▆████▇▆▆███████████████▇▇▅▅▅▇▆▇█████▇▇███▇▅ █
288 ns Histogram: log(frequency) by time 386 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.A42()))BenchmarkTools.Trial: 10000 samples with 131 evaluations per sample.
Range (min … max): 728.237 ns … 58.185 μs ┊ GC (min … max): 0.00% … 98.27%
Time (median): 777.565 ns ┊ GC (median): 0.00%
Time (mean ± σ): 783.360 ns ± 576.843 ns ┊ GC (mean ± σ): 0.73% ± 0.98%
▆▇▄▃ ▄█▇▄▃▄▅▃▂▁▄▄▂▁ ▂ ▁▂▃▂▁▁ ▂
█████▆▅▇▃▅▅▄▃▄▁▄▄█████████████████▇▅▃▅▃▅█████████▇███▇▇▇▆▅▄▅▅ █
728 ns Histogram: log(frequency) by time 888 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.Bisection()))BenchmarkTools.Trial: 10000 samples with 10 evaluations per sample.
Range (min … max): 1.609 μs … 3.655 μs ┊ GC (min … max): 0.00% … 0.00%
Time (median): 1.626 μs ┊ GC (median): 0.00%
Time (mean ± σ): 1.686 μs ± 140.655 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
██▃▁▁▁ ▄▆▅▂▁ ▂
███████▇▅▄▁█████▇▇▆▃▄▃▄▄▄▁▄▃▅▃▃▃▄▃▅██▅▄▄▃▁▃▃▃▁▁▃▁▁▃▃▃▁▄▅▇██ █
1.61 μs Histogram: log(frequency) by time 2.41 μs <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.SuperHalley()))BenchmarkTools.Trial: 10000 samples with 376 evaluations per sample.
Range (min … max): 249.056 ns … 25.259 μs ┊ GC (min … max): 0.00% … 98.39%
Time (median): 276.049 ns ┊ GC (median): 0.00%
Time (mean ± σ): 288.775 ns ± 436.146 ns ┊ GC (mean ± σ): 3.24% ± 2.35%
▅█▇▅▂ ▃▃▂ ▂▃▄▅▆▅▄▃▄▄▅▄▃ ▁▁▁ ▁▁ ▂
███████▆▇▅▆▆▅▄▄▄█████▇▅▅▆▆▅▅▄▄▇██████████████▇▆▅▆▇██████████▇ █
249 ns Histogram: log(frequency) by time 336 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.Brent()))BenchmarkTools.Trial: 10000 samples with 198 evaluations per sample.
Range (min … max): 442.545 ns … 47.333 μs ┊ GC (min … max): 0.00% … 98.62%
Time (median): 490.566 ns ┊ GC (median): 0.00%
Time (mean ± σ): 490.964 ns ± 605.707 ns ┊ GC (mean ± σ): 1.73% ± 1.39%
█▄ ▄▅
▆██▄▃▂▂▂▂▂▂▂▂▂▂▂▂▂▁▁▂▂▂▃▄███▄▅▅▄▃▄▅▄▃▃▃▃▂▂▂▂▂▂▂▂▃▃▃▃▃▂▂▂▂▂▂▂▂ ▃
443 ns Histogram: frequency by time 555 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.Order2()))BenchmarkTools.Trial: 10000 samples with 236 evaluations per sample.
Range (min … max): 318.648 ns … 40.968 μs ┊ GC (min … max): 0.00% … 98.61%
Time (median): 367.297 ns ┊ GC (median): 0.00%
Time (mean ± σ): 369.799 ns ± 652.231 ns ┊ GC (mean ± σ): 3.02% ± 1.71%
▆█▇▄▁ ▂▂▁ ▃▆▇▆▅▆▆▅▄▄▄▃▃▄▄▂ ▁▁ ▁▁ ▂
█████▇▄▆█▆▅▄▄▄▅▂▄▄▂▄▇█████████████████████▆▄▅▄▅███████████▇▇▇ █
319 ns Histogram: log(frequency) by time 426 ns <
Memory estimate: 128 bytes, allocs estimate: 1.@benchmark orbitsolve(orb, t, PlanetOrbits.RootsMethod(Roots.AlefeldPotraShi()))BenchmarkTools.Trial: 10000 samples with 173 evaluations per sample.
Range (min … max): 617.110 ns … 53.893 μs ┊ GC (min … max): 0.00% … 98.40%
Time (median): 664.538 ns ┊ GC (median): 0.00%
Time (mean ± σ): 668.868 ns ± 698.711 ns ┊ GC (mean ± σ): 1.46% ± 1.39%
▃█ ▄▂ ▁
██▆▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃██▅▄██▄▂▃▃▂▁▂▃▂▂▁▁▁▁▁▁▂▂▂▂▁▂▂▁▁▁▁▁▁▁▁▁▁▁ ▂
617 ns Histogram: frequency by time 747 ns <
Memory estimate: 128 bytes, allocs estimate: 1.High precision
You can solve Kepler's equation in high precision using big floats and tightening the tolerance on the solver.
orb_big = orbit(a=big(1.2), e=big(0.1), M=big(1.0), ω=big(1.4), τ=big(0.5))
sol = orbitsolve(orb_big, big(t), PlanetOrbits.RootsMethod(Roots.Thukral5B(),rtol=1e-30,atol=1e-30,))
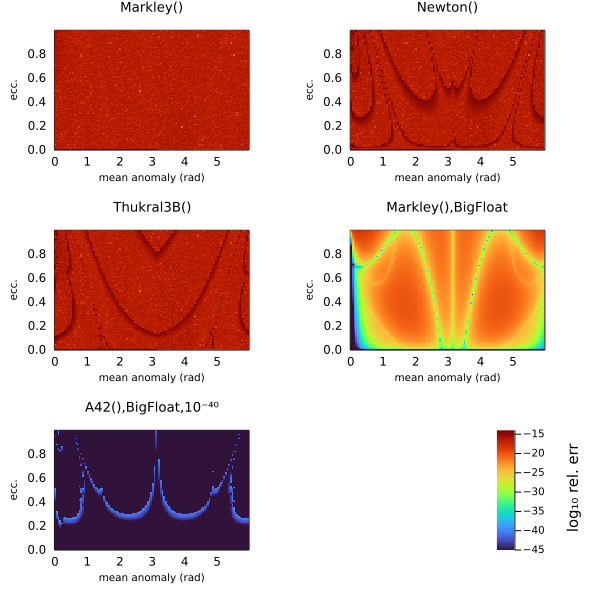
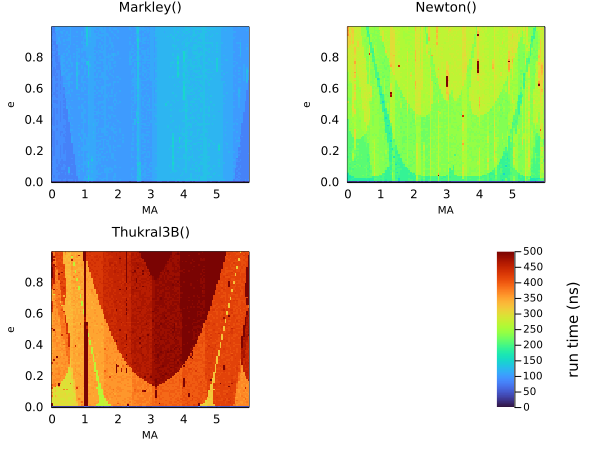
radvel(sol)24650.95447361446997022436542900109713321175234563222583018047585031821959181256Comparison